题目内容
已知(x-m)7=a0+a1x+a2x2+…+a7x7的展开式中x4的系数是-35,则m=
1
1
;a1+a2+a3+…+a7=1
1
.分析:在二项展开式的通项公式中,令x的指数等于4,求出r的值,根据x4的系数是-35,即可求得m的值.求出a0的值,再把x=1和m=1代入二项式及其展开式,可得a1+a2+a3+…+a7的值.
解答:解:二项展开式的通项为Tr+1=
x7-r (-m)r,令7-r=4,可得r=3.
故
(-m)3=-35,解得m=1.
故常数项为
(-1)7=-1=a0,
∴(1-1)7=a0+a1+a2+…+a7=0,
∴a1+a2+a3+…+a7=-a0=1,
故答案为 1; 1.
| C | r 7 |
故
| C | 3 7 |
故常数项为
| C | 7 7 |
∴(1-1)7=a0+a1+a2+…+a7=0,
∴a1+a2+a3+…+a7=-a0=1,
故答案为 1; 1.
点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
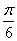 )),设g(x)=m·n(a∈R,且a为常数),
)),设g(x)=m·n(a∈R,且a为常数),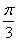 )上的最大值与最小值之和为7,求a的值。
)上的最大值与最小值之和为7,求a的值。