题目内容
已知各项都不相等的等差数列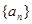 的前六项和为60,且
的前六项和为60,且 的等比中项.
的等比中项.
(I)求数列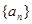 的通项公式
的通项公式 ;
;
(II)若数列 的前n项和
的前n项和 .
.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)根据题意,设出等差数列的公差,利用题中等差数列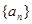 的前六项和为60,且
的前六项和为60,且 为
为 和
和 的等比中项求出
的等比中项求出 和
和 ,再利用题型公式和前
,再利用题型公式和前 项和公式求出
项和公式求出 和
和 ;(2)根据
;(2)根据 ,可选择累加法求出数列的通项公式,代入到
,可选择累加法求出数列的通项公式,代入到 ,根据其特征,利用裂项相消法求出最终的结果.
,根据其特征,利用裂项相消法求出最终的结果.
试题解析:(1)设数列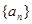 的公差是
的公差是 ,则
,则 ,即
,即 ①
① ,即
,即 ②
②
由①②解得


由(1)知


……
累加,得



所以
则
所以


考点:1.等差数列基本量的求解;2.数列的通项公式的求法;3.数列的求和公式.

练习册系列答案
相关题目
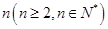 的两个数列
的两个数列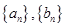 满足
满足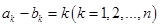 且集合
且集合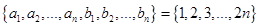 ,则称数列
,则称数列 项相关数列”.
项相关数列”.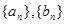 是一对“4项相关数列”,求
是一对“4项相关数列”,求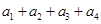 和
和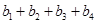 的值,并写出一对“
的值,并写出一对“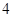 项相
项相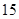 项相关数列”
项相关数列”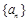 的前n项和为
的前n项和为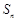 ,且
,且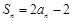 .
.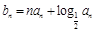 ,数列
,数列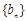 的前n项和为
的前n项和为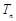 ,若不等式
,若不等式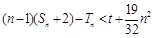 对任意
对任意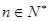 恒成立,求实数
恒成立,求实数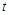 的取值范围.
的取值范围. 中,
中,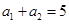 ,
,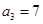 ,记数列
,记数列 的前
的前 项和为
项和为 .
. 、
、 ,使得
,使得 、
、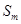 、
、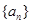 中,
中,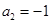 且
且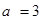 求等差数列
求等差数列 为等差数列,
为等差数列, 是等差数列的前
是等差数列的前 项和,已知
项和,已知 ,
, .
. ;(2)
;(2) 为数列
为数列 的前
的前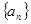 是等差数列,且
是等差数列,且
 求数列
求数列 前n项和的公式.
前n项和的公式. 中
中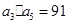 ,
, ,求
,求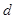 ;
; .
. 为等差数列,且
为等差数列,且
 ;
; 成等比数列,求数列
成等比数列,求数列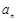 .
.