题目内容
2．求函数y=$\frac{\sqrt{x+2}}{\sqrt{6-2x}-1}$的定义域，并用区间表示．分析 根据二次根式的性质得到不等式组，解出即可．
解答 解：由题意得：
$\left\{\begin{array}{l}{x+2≥0}\\{6-2x≥0}\\{6-2x≠1}\end{array}\right.$，解得：-2≤x≤3且x≠$\frac{5}{2}$．
∴函数的定义域是：[-2，$\frac{5}{2}$）∪（$\frac{5}{2}$，3]．
点评 本题考查了求函数的定义域问题，考查不等式组的解法，是一道基础题．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
相关题目
17．圆心在y轴上，且过点（-1，2）并切于x轴的圆的标准方程为（ ）
| A． | （x-$\frac{5}{4}$）2+y2=$\frac{25}{16}$ | B． | （x）2+（y-$\frac{5}{4}$）2=$\frac{25}{16}$ | C． | （x+$\frac{5}{4}$）2+y2=$\frac{25}{16}$ | D． | （x）2+（y+$\frac{5}{4}$）2=$\frac{25}{16}$ |
7．
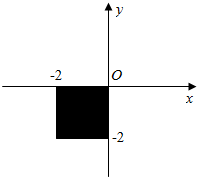用描述法表示下图所示阴影部分的点（包括边界上的点）的坐标的集合是（ ）
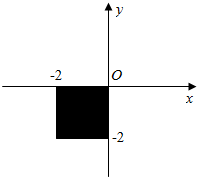用描述法表示下图所示阴影部分的点（包括边界上的点）的坐标的集合是（ ）| A． | {-2≤x≤0且-2≤y≤0} | B． | {（x，y）|-2≤x≤0且-2≤y≤0} | ||
| C． | {（x，y）|-2≤x≤0且-2≤y＜0} | D． | {（x，y）|-2≤x≤0或-2≤y≤0} |
14．等比数列{an}的前n项和为Sn=x3n-1-2，则x=（ ）
| A． | $\frac{1}{3}$ | B． | -6 | C． | -$\frac{1}{3}$ | D． | 6 |