题目内容
已知集合 .则A∩B为
.则A∩B为
- A.{x|-1≤x≤1}
- B.{x|-1<x<1}
- C.{x|-1<x≤1}
- D.{x|-1<x≤2}
C
分析:解分式不等式求出A={x|-1<x≤2},根据余弦函数的值域求出B={y|-1≤y≤1},再根据两个集合的交集的定义
求出 A∩B.
解答:A={x|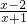 ≤0 }={x|-1<x≤2},B={y|y=cosx}={y|-1≤y≤1},
≤0 }={x|-1<x≤2},B={y|y=cosx}={y|-1≤y≤1},
∴A∩B={x|-1<x≤2}∩{x|-1≤x≤1}={x|-1<x≤1},
故选C.
点评:本题主要考查分式不等式的解法,体现了化归与转化的数学思想,两个集合的交集的定义和求法,属于基础题.
分析:解分式不等式求出A={x|-1<x≤2},根据余弦函数的值域求出B={y|-1≤y≤1},再根据两个集合的交集的定义
求出 A∩B.
解答:A={x|
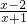 ≤0 }={x|-1<x≤2},B={y|y=cosx}={y|-1≤y≤1},
≤0 }={x|-1<x≤2},B={y|y=cosx}={y|-1≤y≤1},∴A∩B={x|-1<x≤2}∩{x|-1≤x≤1}={x|-1<x≤1},
故选C.
点评:本题主要考查分式不等式的解法,体现了化归与转化的数学思想,两个集合的交集的定义和求法,属于基础题.

练习册系列答案
相关题目
 ,则A∩B为( )
,则A∩B为( )


 .则A∩B为( )
.则A∩B为( )