题目内容
双曲线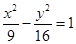 上有一点P到左准线的距离为
上有一点P到左准线的距离为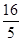 ,则P到右焦点的距离为 。
,则P到右焦点的距离为 。
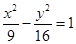 上有一点P到左准线的距离为
上有一点P到左准线的距离为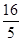 ,则P到右焦点的距离为 。
,则P到右焦点的距离为 。
【错解分析】设F1、F2分别为由双曲线的左、右焦点,则由双曲线的方程为
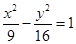 ,易求得a=3,c=5,从而离心率e=
,易求得a=3,c=5,从而离心率e= ,再由第二定义,易求|PF1|=ed1=
,再由第二定义,易求|PF1|=ed1= ,于是又由第一定义
,于是又由第一定义 ,得|PF2|=
,得|PF2|= 。
。【正解】P若在右支上,则其到F1的最短距离应为右顶点A2到F1的距离| A2 F1|=a+c=8,而
 ,故点P只能在左支,于是|PF2|=
,故点P只能在左支,于是|PF2|= 。
。
练习册系列答案
相关题目
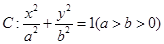 的离心率为
的离心率为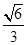 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为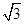 .
.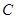 的方程;
的方程;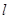 与椭圆
与椭圆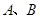 两点,坐标原点
两点,坐标原点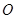 到直线
到直线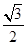 ,求
,求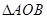
 的焦点与双曲线
的焦点与双曲线 的右焦点重合.
的右焦点重合.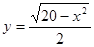 与直线L:
与直线L: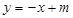 仅有一个公共点,求m的范围.
仅有一个公共点,求m的范围.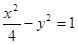 的两个焦点,点在双曲线上且满足
的两个焦点,点在双曲线上且满足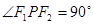 ,则
,则 的面积是( )。
的面积是( )。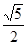
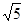
 的坐标分别是
的坐标分别是 ,直线
,直线 相交于点
相交于点 ,且直线
,且直线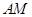 与直线
与直线 的斜率之差是
的斜率之差是 ,则点
,则点
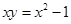


 ,焦点在x轴上的椭圆;
,焦点在x轴上的椭圆; 的左顶点.
的左顶点. 的离心率为
的离心率为 ,则双曲线
,则双曲线 的离心率为
的离心率为
