题目内容
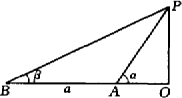
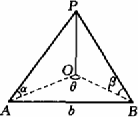
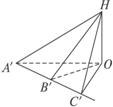
如图，为了测量某塔的高度，某人在一条水平公路C、D两点处进行测量．在C点测得塔顶A在南偏西80°，仰角为45°，此人沿着南偏东40°方向前进10米到D点，测得塔顶的仰角为30°，试求塔的高度．分析：设塔高AB=x，根据题意得Rt△ABC中，BC=AB=x，可得Rt△ABD中，由∠ADB=30°算出BD=
x，最后在△BCD中由余弦定理建立关于x的方程，解之可得x=10，从而得到塔的高度．
| 3 |
解答：解：由题意得，AB⊥平面BCO
∵BC、BD?平面BCO，∴AB⊥BC，AB⊥BD．（2分）
设塔高AB=x，（3分）
在Rt△ABC中，∠ACB=45°，可得BC=AB=x，（5分）
在Rt△ABD中，∠ADB=30°，∴BD=
=
x，（8分）
在△BCD中由余弦定理，得BD2=CB2+CD2-2CB•CDcos120°，
∴(
x)2=x2+100+10x，
解得x=10或=-5（舍去）．（11分）
答：塔高为10米．（12分）
∵BC、BD?平面BCO，∴AB⊥BC，AB⊥BD．（2分）
设塔高AB=x，（3分）
在Rt△ABC中，∠ACB=45°，可得BC=AB=x，（5分）
在Rt△ABD中，∠ADB=30°，∴BD=
| AB |
| tan30° |
| 3 |
在△BCD中由余弦定理，得BD2=CB2+CD2-2CB•CDcos120°，
∴(
| 3 |
解得x=10或=-5（舍去）．（11分）
答：塔高为10米．（12分）
点评：本题给出实际应用问题，求塔的高度．着重考查了线面垂直的定义、直角三角形的性质和正余弦定理等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
