题目内容
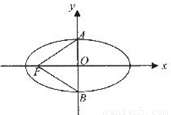
如图，椭圆C：
=1（a＞b＞0）的左焦点为
，上下顶点分别为A，B，已知△AFB是等边三角形．（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F作倾斜角为α的直线l交椭圆C于M、N两点，求证：|MN|=
．
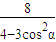【答案】分析：（I）利用左焦点为
，上下顶点分别为A，B，△AFB是等边三角形，求出几何量，即可求椭圆C的方程；
（Ⅱ）分类讨论，设出直线方程，代入椭圆方程，利用韦达定理，计算|MN|，即可得到结论．
解答：（I）解：由题意，
，
，∴b=2
∴
=4
∴椭圆C的方程为
；
（Ⅱ）证明：当
时，设k=tanα，l：
代入
，可得（1+4k2）x2+
x+48k2-16=0
设M（x1，y1），N（x2，y2），则x1+x2=-
，x1x2=
∴|x1-x2|=
=
∴|MN|=
=
=
=
当
时，|MN|=2，
=2，∴|MN|=
．
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查弦长的计算，属于中档题．
，上下顶点分别为A，B，△AFB是等边三角形，求出几何量，即可求椭圆C的方程；（Ⅱ）分类讨论，设出直线方程，代入椭圆方程，利用韦达定理，计算|MN|，即可得到结论．
解答：（I）解：由题意，
，，∴b=2∴
=4∴椭圆C的方程为
；（Ⅱ）证明：当
时，设k=tanα，l：代入
，可得（1+4k2）x2+x+48k2-16=0设M（x1，y1），N（x2，y2），则x1+x2=-
，x1x2=∴|x1-x2|=
=∴|MN|=
===当
时，|MN|=2，=2，∴|MN|=．点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查弦长的计算，属于中档题．
练习册系列答案
相关题目
如图，椭圆C：
+
=1（a＞b＞0）的左右顶点为A1，A2，左右焦点为F1，F2，其中F1，F2是A1A2的三等分点，A是椭圆上任意一点，且|AF1|+|AF2|=6．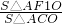
，n=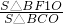
，若点A在第一象限，求m+n的取值范围．
+
=1的右顶点是A，上下两个顶点分别为B，D，四边形DAMB是矩形（O为坐标原点），点E，P分别是线段OA，MA的中点．
求证：直线SR过定点，并求出此定点的坐标．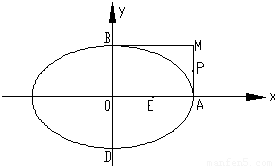
如图，椭圆C：
+
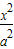=1（a＞b＞0）的焦点F1，F2和短轴的一个端点A构成等边三角形，点（
，
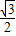）在椭圆C上，直线l为椭圆C的左准线．
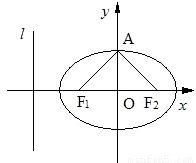如图，椭圆C：
+
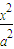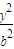=1（a＞b＞0）的焦点F1，F2和短轴的一个端点A构成等边三角形，点（
，
）在椭圆C上，直线l为椭圆C的左准线．