Question

1．求证：正三棱柱三个侧面的三条两两异面的对角线中，只要有一对互相垂直，另两对也互相垂直．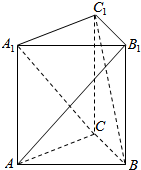

Answer 1

分析 如图所示，设A₁C⊥BC₁，建立如图所示的坐标系，正三棱柱底面边长与高分别为2a、b，证明数量积为0，即可证明结论．

解答 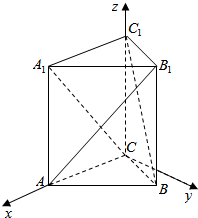证明：如图所示，设A₁C⊥BC₁，建立如图所示的坐标系，正三棱柱底面边长与高分别为2a、b，则A₁（2a，0，b），C（0，0，0），B（a，$\sqrt{3}$a，0），C₁（0，0，b），A（2a，0，0），B₁（a，$\sqrt{3}$a，b），
∴$\overrightarrow{{A}_{1}C}$=（-2a，0，-b），$\overrightarrow{B{C}_{1}}$=（-a，-$\sqrt{3}$a，b），
∵A₁C⊥BC₁，∴$\overrightarrow{{A}_{1}C}$•$\overrightarrow{B{C}_{1}}$=2a²-b²=0，
∵$\overrightarrow{A{B}_{1}}$=（-a，$\sqrt{3}$a，b），
∴$\overrightarrow{{A}_{1}C}$•$\overrightarrow{A{B}_{1}}$=2a²-b²=0，$\overrightarrow{A{B}_{1}}$•$\overrightarrow{B{C}_{1}}$=-2a²+b²=0，
∴A₁C⊥AB₁，AB₁⊥BC₁．

点评 本题考查线线垂直，考查向量知识的运用，正确建立坐标系，求向量是关键．