题目内容
求证:斜边上的高、斜边上的中线对应成比例的两直角三角形相似.如图,已知Rt△ABC,∠C=90°,Rt△A′B′C′,∠C′=90°,CD、CE、C′D′、C′E′分别是它们斜边上的高和中线,且![]() .
.
求证:Rt△ABC∽Rt△A′B′C′.
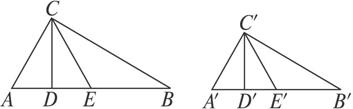
图
证明:在Rt△CDE和△C′D′E′中,
∵![]() ,∴Rt△CDE∽Rt△C′D′E′.
,∴Rt△CDE∽Rt△C′D′E′.
∴∠CED=∠C′E′D′.
又∵CE是斜边中线,∴CE=![]() AB=BE.∴∠ECB=∠B.
AB=BE.∴∠ECB=∠B.
又∵∠B+∠ECB=∠CED,∴∠B=![]() ∠CED,
∠CED,
同理,∠B′=![]() ∠C′E′D′.∴∠B=∠B′.
∠C′E′D′.∴∠B=∠B′.
∴Rt△ABC∽Rt△A′B′C′.

练习册系列答案
相关题目
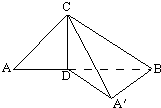 CD是直角三角形ABC斜边上的高,BD=2AD,将△ACD绕CD旋转到△A′CD,使二面角A′-CD-B为60°.
CD是直角三角形ABC斜边上的高,BD=2AD,将△ACD绕CD旋转到△A′CD,使二面角A′-CD-B为60°.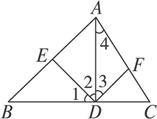
 中,
中, ,
,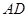 斜边
斜边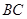 上的高,以
上的高,以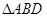 折
起,使
折
起,使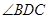 为直角。
为直角。 平面
平面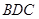 ;(2)求证:
;(2)求证: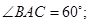
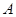 到平面
到平面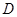 到平面
到平面 的距离;
的距离;