题目内容
.(本小题满分14分)已知函数 对任意实数
对任意实数 均有
均有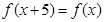 ,当
,当 时,
时, 是正比例函数,当
是正比例函数,当 时,
时, 是二次函数,且在
是二次函数,且在 时
时 取最小值
取最小值 。
。
(1)证明: ;
;
(2)求出 在
在 的表达式;并讨论
的表达式;并讨论 在
在 的单调性。
的单调性。
 对任意实数
对任意实数 均有
均有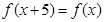 ,当
,当 时,
时, 是正比例函数,当
是正比例函数,当 时,
时, 是二次函数,且在
是二次函数,且在 时
时 取最小值
取最小值 。
。(1)证明:
 ;
;(2)求出
 在
在 的表达式;并讨论
的表达式;并讨论 在
在 的单调性。
的单调性。(1)∵当 时,
时, 是正比例函数,
是正比例函数,
∴设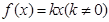
∴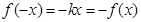 ∴
∴ 为奇函数。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
为奇函数。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
∵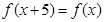 ∴
∴ 的周期
的周期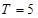 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3分
∴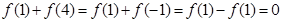 。。。。。。。。。。。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。。。。。。。。。。。5分
(2)当 时,依题意可设
时,依题意可设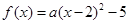
由(1)有
∴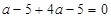 ,得
,得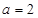 ∴
∴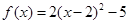 。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。7分
当 时,
时,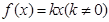 ∴
∴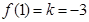 ∴
∴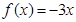 。。。。。。。。。8分
。。。。。。。。。8分
当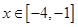 时,
时,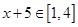 ,∴
,∴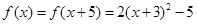 。。。。。。。9分
。。。。。。。9分
综上: 在
在 的表达式为
的表达式为 =
=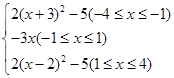 。。。。。。。10分
。。。。。。。10分
作出 的图象(如右图)。。。。。。。。。。12分
的图象(如右图)。。。。。。。。。。12分
由图象可知 在
在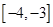 和
和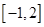 上是减函数,在
上是减函数,在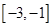 和
和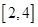 上是增函数。14分
上是增函数。14分
 时,
时, 是正比例函数,
是正比例函数,∴设
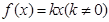
∴
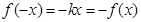 ∴
∴ 为奇函数。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
为奇函数。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分∵
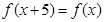 ∴
∴ 的周期
的周期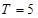 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3分∴
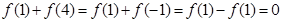 。。。。。。。。。。。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。。。。。。。。。。。5分(2)当
 时,依题意可设
时,依题意可设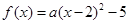
由(1)有

∴
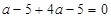 ,得
,得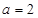 ∴
∴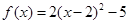 。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。7分当
 时,
时,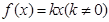 ∴
∴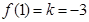 ∴
∴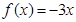 。。。。。。。。。8分
。。。。。。。。。8分当
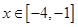 时,
时,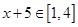 ,∴
,∴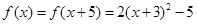 。。。。。。。9分
。。。。。。。9分综上:
 在
在 的表达式为
的表达式为 =
=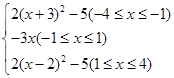 。。。。。。。10分
。。。。。。。10分作出
 的图象(如右图)。。。。。。。。。。12分
的图象(如右图)。。。。。。。。。。12分由图象可知
 在
在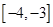 和
和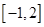 上是减函数,在
上是减函数,在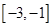 和
和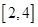 上是增函数。14分
上是增函数。14分略

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
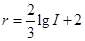 。1976年7月28日,我国唐山发生了里氏震级为7.8级的地震,它所释放的相对能量是2010年2月27日智利地震所散发的相对能量的
。1976年7月28日,我国唐山发生了里氏震级为7.8级的地震,它所释放的相对能量是2010年2月27日智利地震所散发的相对能量的 倍,那么智利地震的里氏震级是 级。(取lg2=0.3)
倍,那么智利地震的里氏震级是 级。(取lg2=0.3) 在区间
在区间
 为整数)上的值域是
为整数)上的值域是 ,则满足条件的数对
,则满足条件的数对 共有 ▲ 对;
共有 ▲ 对;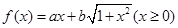 的图像经过(o,1),且
的图像经过(o,1),且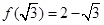
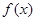 的值域;
的值域;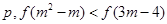 ,命题q:函数
,命题q:函数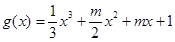 在R上无极值,是否存在实数m满足复合命题p且q为真命题?若存在,求出m的范围;若不存在,说明理由.
在R上无极值,是否存在实数m满足复合命题p且q为真命题?若存在,求出m的范围;若不存在,说明理由.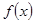 是定义在实数集R上的奇函数,当
是定义在实数集R上的奇函数,当 >0时,
>0时,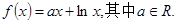
 函数
函数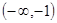 上是单调减函数,求a的取值范围;
上是单调减函数,求a的取值范围;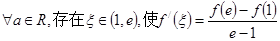 .
.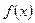 满足:
满足: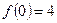 ,
,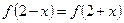 ,且该函数的最小值为1.
,且该函数的最小值为1.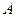 =
= 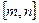 .(其中
.(其中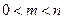 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数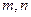 ,使得函数
,使得函数 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为 的函数;并求自变量
的函数;并求自变量
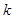 ,如果关于
,如果关于 的方程
的方程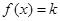 最多有
最多有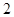 个不同的实数解,则
个不同的实数解,则 (
( 为实常数)的不同的实数解的个数最多为 .
为实常数)的不同的实数解的个数最多为 .