题目内容
已知向量
=（1，2），
=（-2，1），k，t为正实数，
=+
，
=
+
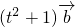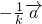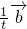，问是否存在实数k、t，使∥，若存在，求出k的取值范围；若不存在，请说明理由．
解：∵
=（1，2）+（t2+1）（-2，1）=（-2t2-1，t2+3），
=-
（1，2）+
（-2，1）
=
假设存在正实数k，t使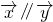
，则
（-2t2-1）（-
+）-（t2+3）（--
）=0，
化简得
+=0，即t3+t+k=0，
∵k，t是正实数，故满足上式的k，t不存在，
∴不存在这样的正实数k，t，使．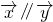
分析：先计算出向量的坐标，再利用向量共线的充要条件即可得出．
点评：熟练掌握向量的运算和共线的充要条件是解题的关键．
=（1，2）+（t2+1）（-2，1）=（-2t2-1，t2+3），
=-
（1，2）+（-2，1）=
假设存在正实数k，t使
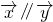，则（-2t2-1）（-
+）-（t2+3）（--）=0，化简得
+=0，即t3+t+k=0，∵k，t是正实数，故满足上式的k，t不存在，
∴不存在这样的正实数k，t，使
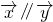．分析：先计算出向量的坐标，再利用向量共线的充要条件即可得出．
点评：熟练掌握向量的运算和共线的充要条件是解题的关键．
练习册系列答案
相关题目
已知向量
=（1，2），
=（x，2），则向量
+2
与2
-
（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、垂直的必要条件是x=-2 | ||
B、垂直的充要条件是x=
| ||
| C、平行的充分条件是x=-2 | ||
| D、平行的充要条件是x=1 |