题目内容
数列![]() ,
,![]() (
(![]() )由下列条件确定:①
)由下列条件确定:①![]() ;②当
;②当![]() 时,
时,![]() 与
与![]() 满足:当
满足:当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() .
.
(Ⅰ)若![]() ,
,![]() ,写出
,写出![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)在数列![]() 中,若
中,若![]() (
(![]() ,且
,且![]() ),试用
),试用![]() 表示
表示![]()
![]() ;
;
(Ⅲ)在(Ⅰ)的条件下,设数列![]()
![]() 满足
满足![]() ,
,![]() ,
,
![]() (其中
(其中![]() 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当![]() 时,恒有
时,恒有![]() .
.
解: (Ⅰ)由题得过两点![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() .………… 1分
.………… 1分
因为![]() ,所以
,所以![]() ,
,![]() .
.
设椭圆方程为![]() ,
,
由 消去
消去![]() 得,
得,![]() .
.
又因为直线![]() 与椭圆
与椭圆![]() 相切,所以
相切,所以![]() ,解得
,解得![]() .
.
所以椭圆方程为![]() . ……………………………………………… 5分
. ……………………………………………… 5分
(Ⅱ)易知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,…………………… 6分
,…………………… 6分
由 消去
消去![]() ,整理得
,整理得![]() . ………… 7分
. ………… 7分
由题意知![]() ,
,
解得![]() . ……………………………………………………………… 8分
. ……………………………………………………………… 8分
设![]() ,
,![]() ,则
,则![]() ,
,![]() . …… 9分
. …… 9分
又直线![]() 与椭圆
与椭圆![]() 相切,
相切,
由 解得
解得![]() ,所以
,所以![]() . ……………………………10分
. ……………………………10分
则![]() . 所以
. 所以![]() .
.
又![]()
![]()
![]()
![]()
![]()
![]()
所以![]() ,解得
,解得![]() .经检验成立. …………………… 13分
.经检验成立. …………………… 13分
所以直线![]() 的方程为
的方程为![]() . …………………… 14分
. …………………… 14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, (
( )由下列条件确定:①
)由下列条件确定:① ;②当
;②当 时,
时, 与
与 满足:当
满足:当 时,
时, ,
, ;当
;当 时,
时, ,
, .
. ,
, ,写出
,写出 ,并求数列
,并求数列 的通项公式;
的通项公式;  (
(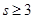 ,且
,且 ),试用
),试用 表示
表示
 ;
;
 满足
满足 ,
, ,
, (其中
(其中 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当 时,恒有
时,恒有 .
.