题目内容
数列{xn}由下列条件确定:x1=a>0,xn+1=(1)证明对n≥2总有xn≥![]() ;
;
(2)证明对n≥2总有xn≥xn+1.
证明:(1)构造函数f(x)=![]() (x+
(x+![]() ),易知f(x)在[
),易知f(x)在[![]() ,+∞)上是增函数.?
,+∞)上是增函数.?
于是xk+1=![]() (xk+
(xk+![]() )在[
)在[![]() ,+∞)上递增,故xk+1≥f(
,+∞)上递增,故xk+1≥f(![]() )=
)=![]() .?
.?
(2)有xn-xn+1=![]() (xn-
(xn-![]() ),?
),?
构造函数f(x)=![]() (x-
(x-![]() ),它在[a,+∞)上是增函数,故有xn-xn+1=
),它在[a,+∞)上是增函数,故有xn-xn+1=![]() (xn-
(xn-![]() )≥f(a)=0,得证.
)≥f(a)=0,得证.

练习册系列答案
相关题目
 ,
, (
( )由下列条件确定:①
)由下列条件确定:① ;②当
;②当 时,
时, 与
与 满足:当
满足:当 时,
时, ,
, ;当
;当 时,
时, ,
, .
. ,
, ,写出
,写出 ,并求数列
,并求数列 的通项公式;
的通项公式;  (
(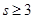 ,且
,且 ),试用
),试用 表示
表示
 ;
;
 满足
满足 ,
, ,
, (其中
(其中 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当 时,恒有
时,恒有 .
.