Question

已知≤x≤,则

(1)1-x的取值范围是［，］；

（2）x(1-x)的取值范围是［，］.

以上命题是否正确？若错误,予以纠正；若正确，请证明.

Answer 1

解：（1）正确.∵≤x≤,

∴-≤-x≤-.

∴1-≤1-x≤1-,即≤1-x≤.

(2)错误.不能由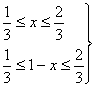,这是因为x与1-x不可能同时取到或,故结论错误.

正确的是:x(1-x)的取值范围是［,］.

证明如下：令y=x(1-x),

则y=-(x-)²+,

∵≤x≤，故有y_min=,y_max=.

温馨提示

    本题型主要考查不等式的性质，常用的解法是正确使用不等式的性质进行直接推导，并注意不等式性质成立的条件和函数性质的应用，以及等价转化的思想，比如减法可转化为加法，除法可转化为乘法等.