题目内容
(13分)(理科)已知双曲线 与椭圆
与椭圆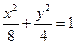 有公共焦点,且以抛物线
有公共焦点,且以抛物线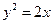 的准线为双曲线
的准线为双曲线 的一条准线.动直线
的一条准线.动直线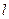 过双曲线
过双曲线 的右焦点
的右焦点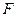 且与双曲线的右支交于
且与双曲线的右支交于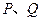 两点.
两点.
(1)求双曲线 的方程;
的方程;
(2)无论直线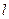 绕点
绕点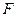 怎样转动,在双曲线
怎样转动,在双曲线 上是否总存在定点
上是否总存在定点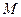 ,使
,使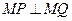 恒成立?若存在,求出点
恒成立?若存在,求出点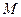 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 与椭圆
与椭圆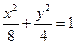 有公共焦点,且以抛物线
有公共焦点,且以抛物线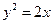 的准线为双曲线
的准线为双曲线 的一条准线.动直线
的一条准线.动直线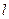 过双曲线
过双曲线 的右焦点
的右焦点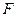 且与双曲线的右支交于
且与双曲线的右支交于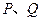 两点.
两点.(1)求双曲线
 的方程;
的方程;(2)无论直线
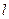 绕点
绕点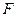 怎样转动,在双曲线
怎样转动,在双曲线 上是否总存在定点
上是否总存在定点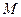 ,使
,使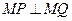 恒成立?若存在,求出点
恒成立?若存在,求出点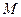 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.(1)

(2)双曲线
 上存在定点
上存在定点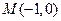 ,使
,使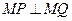 恒成立
恒成立(理科)解:(1)设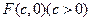 ,则由题意有:
,则由题意有:
 ∴
∴ ,
,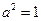 ,
,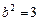
故双曲线 的方程为
的方程为 , ……………4分
, ……………4分
(2)解法一:由(1)得点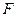 为
为
当直线l的斜率存在时,设直线方程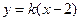 ,
, ,
,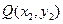
将方程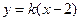 与双曲线方程联立消去
与双曲线方程联立消去 得:
得: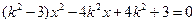 ,
,
∴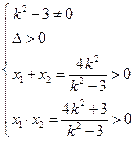 解得
解得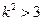 ……………6分
……………6分
假设双曲线 上存在定点
上存在定点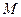 ,使
,使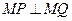 恒成立,设为
恒成立,设为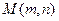
则: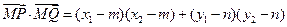
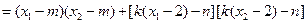
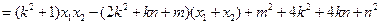
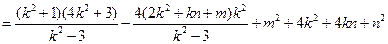
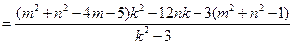
∵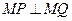 ,∴
,∴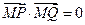 ,
,
故得: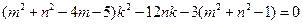 对任意的
对任意的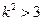 恒成立,
恒成立,
∴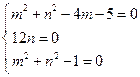 ,解得
,解得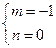
∴当点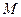 为
为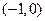 时,
时,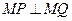 恒成立; ……………10分
恒成立; ……………10分
当直线l的斜率不存在时,由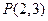 ,
,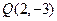 知点
知点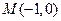 使得
使得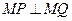 也成立.
也成立.
又因为点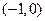 是双曲线
是双曲线 的左顶点, ……………12分
的左顶点, ……………12分
所以双曲线 上存在定点
上存在定点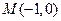 ,使
,使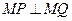 恒成立. ……………13分
恒成立. ……………13分
解法二(略解):当直线l的斜率不存在时,由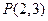 ,
,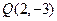 ,
,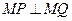 ,且点
,且点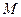 在双曲线
在双曲线 上可求得
上可求得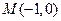 ,
,
当直线l的斜率存在时,将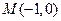 ,
,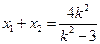 ,
,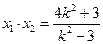 代入
代入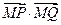 ,经计算发现
,经计算发现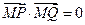 对任意的
对任意的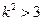 恒成立,从而恒有
恒成立,从而恒有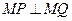 成立.
成立.
因而双曲线 上存在定点
上存在定点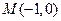 ,使
,使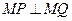 恒成立.
恒成立.
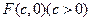 ,则由题意有:
,则由题意有: ∴
∴ ,
,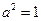 ,
,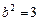
故双曲线
 的方程为
的方程为 , ……………4分
, ……………4分(2)解法一:由(1)得点
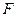 为
为
当直线l的斜率存在时,设直线方程
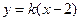 ,
, ,
,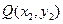
将方程
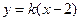 与双曲线方程联立消去
与双曲线方程联立消去 得:
得: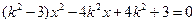 ,
,∴
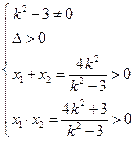 解得
解得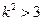 ……………6分
……………6分假设双曲线
 上存在定点
上存在定点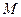 ,使
,使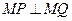 恒成立,设为
恒成立,设为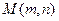
则:
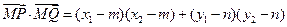
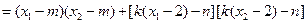
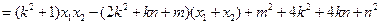
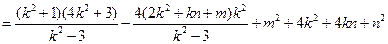
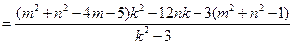
∵
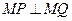 ,∴
,∴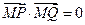 ,
,故得:
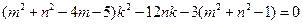 对任意的
对任意的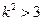 恒成立,
恒成立,∴
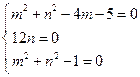 ,解得
,解得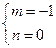
∴当点
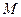 为
为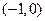 时,
时,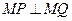 恒成立; ……………10分
恒成立; ……………10分当直线l的斜率不存在时,由
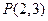 ,
,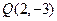 知点
知点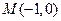 使得
使得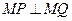 也成立.
也成立.又因为点
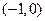 是双曲线
是双曲线 的左顶点, ……………12分
的左顶点, ……………12分所以双曲线
 上存在定点
上存在定点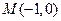 ,使
,使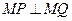 恒成立. ……………13分
恒成立. ……………13分解法二(略解):当直线l的斜率不存在时,由
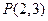 ,
,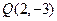 ,
,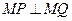 ,且点
,且点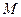 在双曲线
在双曲线 上可求得
上可求得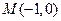 ,
,当直线l的斜率存在时,将
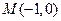 ,
,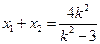 ,
,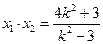 代入
代入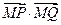 ,经计算发现
,经计算发现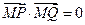 对任意的
对任意的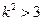 恒成立,从而恒有
恒成立,从而恒有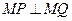 成立.
成立.因而双曲线
 上存在定点
上存在定点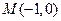 ,使
,使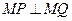 恒成立.
恒成立.
练习册系列答案
相关题目
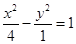 的渐近线方程是
的渐近线方程是 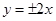
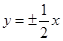
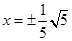
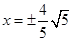
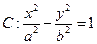 ,F为右焦点,过F作双曲线C在第一、三象限的渐近线的垂线
,F为右焦点,过F作双曲线C在第一、三象限的渐近线的垂线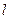 ,若
,若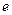 的取值范围为
的取值范围为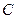 与双曲线
与双曲线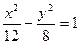 共渐近线,且过点
共渐近线,且过点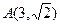 ,则双曲线
,则双曲线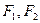 为双曲线
为双曲线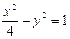 的两个焦点,点
的两个焦点,点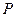 在双曲线上且满足
在双曲线上且满足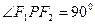 ,则
,则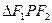 的面积是______________。
的面积是______________。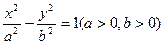 的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )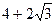
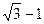
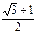
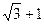
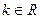 ,则方程
,则方程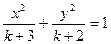 表示焦点在
表示焦点在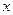 轴上的双曲线的充要条件是( )
轴上的双曲线的充要条件是( )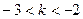
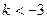
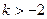
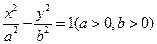 的离心率为
的离心率为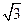 ,右准线方程为
,右准线方程为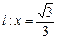 。
。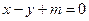 与双曲线
与双曲线 C交于不同的两点A,B,且线段AB的中点在圆
C交于不同的两点A,B,且线段AB的中点在圆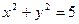 上,求m的值。
上,求m的值。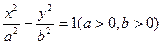 的右顶点为E,过双曲线的左焦点且垂直于
的右顶点为E,过双曲线的左焦点且垂直于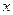 轴的直线与该双曲线相交A、B两点,若
轴的直线与该双曲线相交A、B两点,若 ,则该双曲线的离心率
,则该双曲线的离心率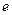 是( )
是( )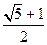 B.2 C.
B.2 C.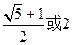 D.不存在
D.不存在