题目内容
【题目】如图,已知等腰直角三角形![]() 的斜边
的斜边![]() 所在直线方程为
所在直线方程为![]() ,其中
,其中![]() 点在
点在![]() 点上方,直角顶点
点上方,直角顶点![]() 的坐标为
的坐标为![]() .
.

(1)求![]() 边上的高线
边上的高线![]() 所在直线的方程;
所在直线的方程;
(2)求等腰直角三角形![]() 的外接圆的标准方程;
的外接圆的标准方程;
(3)分别求两直角边![]() ,
,![]() 所在直线的方程.
所在直线的方程.
【答案】(1)见解析;(2)见解析
【解析】
(1)利用垂直斜率相乘为-1得到CH斜率,点斜式得到CH方程.
(2)首先计算圆心,再计算半径,得到圆的标准方程.
(3)设直线AC方程,通过H到直线的距离计算得到AC,BC直线.
(1)因为等腰直角三角形![]() 的斜边
的斜边![]() 所在直线方程为
所在直线方程为![]() ,设
,设![]() 的斜率为
的斜率为![]()
则![]()
![]() 经过点
经过点![]() ,所以
,所以![]()
(2)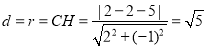
![]() 解得:
解得:![]() ,所以圆心
,所以圆心![]()
所以等腰直角三角形![]() 的外接圆的标准方程为
的外接圆的标准方程为![]()
(3)经判断,![]() 斜率均存在
斜率均存在
设![]() ,即
,即![]() ,因为
,因为![]() 到直线
到直线![]() 的距离为
的距离为![]()
所以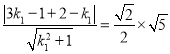
解得:![]() 或
或![]()
因为![]() 点在
点在![]() 点上方,所以
点上方,所以![]()

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目



