题目内容
若函数 在
在 上是减函数,则实数k的取值范围为 .
上是减函数,则实数k的取值范围为 .
【答案】分析:根据对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性可得k>1,且 -k•
-k• +3>0,
+3>0,
由此求得实数k的取值范围.
解答:解:由函数y=x2-kx+3 上是减函数,函数 f(x)=logky 在
上是减函数,函数 f(x)=logky 在 上是减函数,
上是减函数,
可得k>1,且当x= 时,对应的函数值y=
时,对应的函数值y= -k•
-k• +3>0,
+3>0,
由此求得 1<k<2 ,
,
故答案为(1,2 ).
).
点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性,属于中档题.
 -k•
-k• +3>0,
+3>0,由此求得实数k的取值范围.
解答:解:由函数y=x2-kx+3
 上是减函数,函数 f(x)=logky 在
上是减函数,函数 f(x)=logky 在 上是减函数,
上是减函数,可得k>1,且当x=
 时,对应的函数值y=
时,对应的函数值y= -k•
-k• +3>0,
+3>0,由此求得 1<k<2
 ,
,故答案为(1,2
 ).
).点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 在
在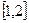 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数 时,函数
时,函数 的最小值是
的最小值是 ,若存在,求出实数
,若存在,求出实数 .
.
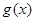 的单调区间;
的单调区间; 在
在 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;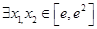 ,使
,使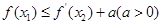 成立,求实数
成立,求实数 在
在 上是减函数,则
上是减函数,则 的取值范围是___.
的取值范围是___. ,
,

 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出
 ,
, 
 在
在 上是减函数,求实数
上是减函数,求实数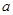 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出