题目内容
函数 .
.
(1)求函数f(x)的最小正周期;
(2)若存在 ,使不等式f(x0)<m成立,求实数m的取值范围.
,使不等式f(x0)<m成立,求实数m的取值范围.
解:(1)∵
= .
.
∴最小正周期T= =π.
=π.
(2)∵ ,∴
,∴ ,
,
∴ ,
,
∴f(x0)的值域为[-1,2].
∵ ,使f(x)<m成立,
,使f(x)<m成立,
∴m>-1,
故实数m的取值范围为(-1,+∞).
分析:(1)利用三角函数的恒等变换化简函数函数f(x)的解析式为 ,从而求出它的最小正周期.
,从而求出它的最小正周期.
(2)根据 ,可得
,可得  ,f(x0)的值域为[-1,2],若存在
,f(x0)的值域为[-1,2],若存在 ,
,
使不等式f(x0)<m成立,m需大于f(x0)的最小值.
点评:本题主要考查三角函数的恒等变换,三角函数的周期性及其求法,三角函数的值域,注意理解“存在 ,使不等式f(x0)<m成立,”的意义,属于中档题.
,使不等式f(x0)<m成立,”的意义,属于中档题.

=
 .
.∴最小正周期T=
 =π.
=π.(2)∵
 ,∴
,∴ ,
,∴
 ,
,∴f(x0)的值域为[-1,2].
∵
 ,使f(x)<m成立,
,使f(x)<m成立,∴m>-1,
故实数m的取值范围为(-1,+∞).
分析:(1)利用三角函数的恒等变换化简函数函数f(x)的解析式为
 ,从而求出它的最小正周期.
,从而求出它的最小正周期.(2)根据
 ,可得
,可得  ,f(x0)的值域为[-1,2],若存在
,f(x0)的值域为[-1,2],若存在 ,
,使不等式f(x0)<m成立,m需大于f(x0)的最小值.
点评:本题主要考查三角函数的恒等变换,三角函数的周期性及其求法,三角函数的值域,注意理解“存在
 ,使不等式f(x0)<m成立,”的意义,属于中档题.
,使不等式f(x0)<m成立,”的意义,属于中档题. 
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
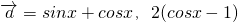 ,
,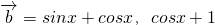 ,函数
,函数 .
.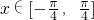 时,求函数f(x)的值域.
时,求函数f(x)的值域.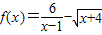 .
.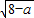
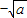 =0,求a的值.
=0,求a的值.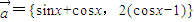 ,
,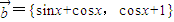 ,函数
,函数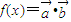 .
.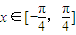 时,求函数f(x)的值域.
时,求函数f(x)的值域.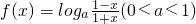 .
.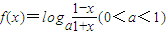 .
.