题目内容
已知函数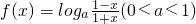 .
.
(1)求函数f(x)的定义域D,并判断f(x)的奇偶性;
(2)如果当x∈(t,a)时,f(x)的值域是(-∞,1),求a与t的值;
(3)对任意的x1,x2∈D,是否存在x3∈D,使得f(x1)+f(x2)=f(x3),若存在,求出x3;若不存在,请说明理由.
解:(1)要使原函数有意义,则 ,解得-1<x<1,
,解得-1<x<1,
所以,函数f(x)的定义域D=(-1,1)
f(x)是定义域内的奇函数.
证明:对任意x∈D,有
所以函数f(x)是奇函数.
另证:对任意x∈D,
所以函数f(x)是奇函数.
(2)由 知,函数
知,函数 在(-1,1)上单调递减,
在(-1,1)上单调递减,
因为0<a<1,所以f(x)在(-1,1)上是增函数
又因为x∈(t,a)时,f(x)的值域是(-∞,1),所以(t,a)⊆(-1,1)
且 在(t,a)的值域是(a,+∞),
在(t,a)的值域是(a,+∞),
故 且t=-1(结合g(x)图象易得t=-1)
且t=-1(结合g(x)图象易得t=-1)
由 得:a2+a=1-a,解得
得:a2+a=1-a,解得 或a=
或a= (舍去).
(舍去).
所以 ,t=-1
,t=-1
(3)假设存在x3∈(-1,1)使得f(x1)+f(x2)=f(x3)
即
则
 ,
,
解得 ,
,
下面证明 .
.
证明:法一、
由 .
.
∵x1,x2∈(-1,1),∴ ,
, ,
,
∴ ,即
,即 ,∴
,∴ .
.
所以存在 ,使得f(x1)+f(x2)=f(x3).
,使得f(x1)+f(x2)=f(x3).
法二、
要证明 ,即证
,即证 ,也即
,也即 .
.
∵x1,x2∈(-1,1),∴ ,∴
,∴ ,
,
∴ .
.
所以存在 ,使得f(x1)+f(x2)=f(x3).
,使得f(x1)+f(x2)=f(x3).
分析:(1)直接由真数大于0,解分式不等式可得函数的定义域,利用定义判断函数的奇偶性;
(2)给出的函数是对数型的复合函数,经分析可知内层分式函数为减函数,外层对数函数也为减函数,要保证
当x∈(t,a)时,f(x)的值域是(-∞,1),首先应有(t,a)⊆(-1,1),且当x∈(t,a)时,
 ∈(a,+∞),结合内层函数图象及单调性可得t=-1,且
∈(a,+∞),结合内层函数图象及单调性可得t=-1,且 ,从而求出a和t的值;
,从而求出a和t的值;
(3)假设存在x3∈D,使得f(x1)+f(x2)=f(x3),代入对数式后把x3用x1,x2表示,只要能够证明x3在定义域内即可,证明可用作差法或分析法.
点评:本题考查了函数的定义域及其求法,考查了复合函数的单调性,考查了复合函数的值域,体现了数学转化思想方法,训练了存在性问题的证明方法,该题综合考查了函数的有关性质,属有一定难度的题目.
 ,解得-1<x<1,
,解得-1<x<1,所以,函数f(x)的定义域D=(-1,1)
f(x)是定义域内的奇函数.
证明:对任意x∈D,有

所以函数f(x)是奇函数.
另证:对任意x∈D,

所以函数f(x)是奇函数.
(2)由
 知,函数
知,函数 在(-1,1)上单调递减,
在(-1,1)上单调递减,因为0<a<1,所以f(x)在(-1,1)上是增函数
又因为x∈(t,a)时,f(x)的值域是(-∞,1),所以(t,a)⊆(-1,1)
且
 在(t,a)的值域是(a,+∞),
在(t,a)的值域是(a,+∞),故
 且t=-1(结合g(x)图象易得t=-1)
且t=-1(结合g(x)图象易得t=-1)由
 得:a2+a=1-a,解得
得:a2+a=1-a,解得 或a=
或a= (舍去).
(舍去).所以
 ,t=-1
,t=-1(3)假设存在x3∈(-1,1)使得f(x1)+f(x2)=f(x3)
即

则

 ,
,解得
 ,
,下面证明
 .
.证明:法一、
由
 .
.∵x1,x2∈(-1,1),∴
 ,
, ,
,∴
 ,即
,即 ,∴
,∴ .
.所以存在
 ,使得f(x1)+f(x2)=f(x3).
,使得f(x1)+f(x2)=f(x3).法二、
要证明
 ,即证
,即证 ,也即
,也即 .
.∵x1,x2∈(-1,1),∴
 ,∴
,∴ ,
,∴
 .
.所以存在
 ,使得f(x1)+f(x2)=f(x3).
,使得f(x1)+f(x2)=f(x3).分析:(1)直接由真数大于0,解分式不等式可得函数的定义域,利用定义判断函数的奇偶性;
(2)给出的函数是对数型的复合函数,经分析可知内层分式函数为减函数,外层对数函数也为减函数,要保证
当x∈(t,a)时,f(x)的值域是(-∞,1),首先应有(t,a)⊆(-1,1),且当x∈(t,a)时,
 ∈(a,+∞),结合内层函数图象及单调性可得t=-1,且
∈(a,+∞),结合内层函数图象及单调性可得t=-1,且 ,从而求出a和t的值;
,从而求出a和t的值;(3)假设存在x3∈D,使得f(x1)+f(x2)=f(x3),代入对数式后把x3用x1,x2表示,只要能够证明x3在定义域内即可,证明可用作差法或分析法.
点评:本题考查了函数的定义域及其求法,考查了复合函数的单调性,考查了复合函数的值域,体现了数学转化思想方法,训练了存在性问题的证明方法,该题综合考查了函数的有关性质,属有一定难度的题目.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.