题目内容
若函数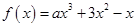 恰有三个单调区间,则实数
恰有三个单调区间,则实数 的取值范围为 ( )
的取值范围为 ( )
A.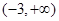 | B.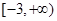 | C.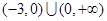 | D.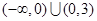 |
C
解析试题分析:由题意知,f′(x)=3ax2+6x-1,
∵f(x)恰有三个单调区间,
∴f′(x)=3ax2+6x-1=0有两个不同的实数根,
∴△=36-4×3a×(-1)>0,且a≠0,即a>-3且a≠0,即(-3,0)∪(0,+∞),故选C.
考点:本题主要考查利用导数研究函数的单调性。
点评:简单题,关键是认识到f′(x)=3ax2+6x-1=0有两个不同的实数根。易错点是忽视对二次项系数的讨论。

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
设函数 的最大值为3,则
的最大值为3,则 的图象的一条对称轴的方程是 ( )
的图象的一条对称轴的方程是 ( )
A. | B. |
C. | D. |
已知函数 在
在 处取极值
处取极值 ,则
,则 =( )
=( )
| A.9 | B. | C. | D. |
已知曲线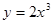 上一点
上一点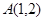 ,则点
,则点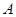 处的切线斜率等于
处的切线斜率等于
A. | B.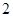 | C.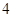 | D.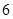 |
设曲线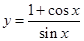 在点
在点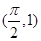 处的切线与直线
处的切线与直线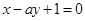 平行,则实数
平行,则实数 等于( )
等于( )
A.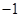 | B.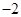 | C.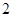 | D.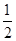 |
过点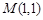 且与曲线
且与曲线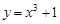 相切的直线方程是( )
相切的直线方程是( )
A.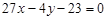 |
B.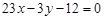 或 或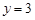 |
C.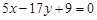 |
D.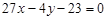 或 或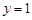 |
已知函数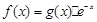 在
在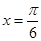 处有极值,则函数
处有极值,则函数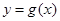 的图象可能是( )
的图象可能是( )
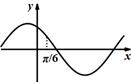
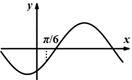

| A. | B. | C. | D. |
曲线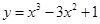 在点
在点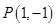 处的切线方程是
处的切线方程是
A.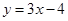 | B.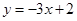 | C.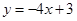 | D.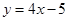 |
一质点沿直线运动,如果由始点起经过t称后的位移为 ,
,
那么速度为零的时刻是( )
| A.0秒 | B.1秒末 | C.2秒末 | D.1秒末和2秒末 |