题目内容
已知椭圆C: 的离心率是
的离心率是 ,其左、右顶点分别为A1,A2,B为短轴的端点,△A1BA2的面积为
,其左、右顶点分别为A1,A2,B为短轴的端点,△A1BA2的面积为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)F2为椭圆C的右焦点,若点P是椭圆C上异于A1,A2的任意一点,直线A1P,A2P与直线x=4分别交于M,N两点,证明:以MN为直径的圆与直线PF2相切于点F2.
(Ⅰ)解:由已知,可得 ,解得a=2,
,解得a=2, . …(4分)
. …(4分)
故所求椭圆方程为 . …(5分)
. …(5分)
(Ⅱ)证明:由(Ⅰ)知A1(-2,0),A2(2,0),F2(1,0).
设 ,则
,则 .
.
于是直线A1P方程为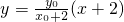 ,令x=4,得
,令x=4,得 ;
;
所以M(4,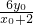 ),同理N(4,
),同理N(4,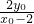 ). …(7分)
). …(7分)
所以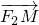 =(3,
=(3,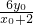 ),
), =(3,
=(3,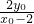 ).
).
所以 =(3,
=(3,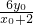 )•(3,
)•(3,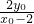 )=
)= =
= =
= .
.
所以F2M⊥F2N,点F2在以MN为直径的圆上. …(9分)
设MN的中点为E,则E(4, ). …(10分)
). …(10分)
又 =(3,
=(3, ),
), ,
,
所以 =(3,
=(3, )
)
= .
.
所以F2E⊥F2P. …(12分)
因为F2E是以MN为直径的圆的半径,E为圆心,F2E⊥F2P,
故以MN为直径的圆与直线PF2相切于右焦点. …(13分)
分析:(Ⅰ)根据椭圆离心率是 ,其左、右顶点分别为A1,A2,B为短轴的端点,△A1BA2的面积为
,其左、右顶点分别为A1,A2,B为短轴的端点,△A1BA2的面积为 ,建立方程组,可求椭圆方程;
,建立方程组,可求椭圆方程;
(Ⅱ)求出M、N的坐标,利用向量证明F2M⊥F2N,点F2在以MN为直径的圆上,确定MN的中点E的坐标,利用向量证明F2E⊥F2P,即可证得以MN为直径的圆与直线PF2相切于右焦点.
点评:本题考查椭圆的标准方程,考查向量知识的运用,解题的关键是确定点的坐标,利用向量的数量积证明垂直关系.
 ,解得a=2,
,解得a=2, . …(4分)
. …(4分)故所求椭圆方程为
 . …(5分)
. …(5分)(Ⅱ)证明:由(Ⅰ)知A1(-2,0),A2(2,0),F2(1,0).
设
 ,则
,则 .
.于是直线A1P方程为
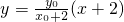 ,令x=4,得
,令x=4,得 ;
;所以M(4,
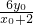 ),同理N(4,
),同理N(4,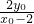 ). …(7分)
). …(7分)所以
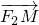 =(3,
=(3,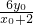 ),
), =(3,
=(3,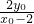 ).
).所以
 =(3,
=(3,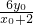 )•(3,
)•(3,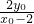 )=
)= =
= =
= .
.所以F2M⊥F2N,点F2在以MN为直径的圆上. …(9分)
设MN的中点为E,则E(4,
 ). …(10分)
). …(10分)又
 =(3,
=(3, ),
), ,
,所以
 =(3,
=(3, )
)
=
 .
.所以F2E⊥F2P. …(12分)
因为F2E是以MN为直径的圆的半径,E为圆心,F2E⊥F2P,
故以MN为直径的圆与直线PF2相切于右焦点. …(13分)
分析:(Ⅰ)根据椭圆离心率是
 ,其左、右顶点分别为A1,A2,B为短轴的端点,△A1BA2的面积为
,其左、右顶点分别为A1,A2,B为短轴的端点,△A1BA2的面积为 ,建立方程组,可求椭圆方程;
,建立方程组,可求椭圆方程;(Ⅱ)求出M、N的坐标,利用向量证明F2M⊥F2N,点F2在以MN为直径的圆上,确定MN的中点E的坐标,利用向量证明F2E⊥F2P,即可证得以MN为直径的圆与直线PF2相切于右焦点.
点评:本题考查椭圆的标准方程,考查向量知识的运用,解题的关键是确定点的坐标,利用向量的数量积证明垂直关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、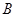 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.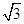
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线