题目内容
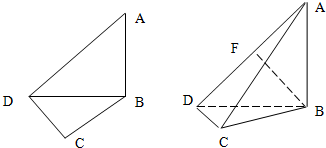
如图,在平面四边形ABCD中,AB=BC=CD=1,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC⊥平面ACD。
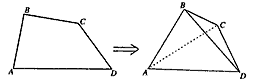
(Ⅰ)求证:平面ABD⊥平面BCD;
(Ⅱ)求二面角B-AD-C的大小。
(Ⅱ)求二面角B-AD-C的大小。
(Ⅰ)证明:∵∠B=90°,
∴AB⊥BC,
∵AB=BC,
∴∠BCA=∠BAC=45°,
又平面四边形ABCD中,∠C=135°,
∴∠DCA=90°,∴DC⊥AC,
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,DC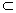 平面ACD,
平面ACD,
∴DC⊥平面ABC,∴AB⊥CD,
∵DC∩BC=C,
∴AB⊥平面BCD,
∵AB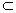 平面ABD,
平面ABD,
∴平面ABD⊥平面PCD。
(Ⅱ)解:设AC的中点为O,连结BO,过O作OE⊥AD于E,连结BE,
∵AB=BC,O为AC的中点,
∴BO⊥AC,
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,BO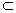 平面ABC,
平面ABC,
∴BO⊥平面ACD,
∵OE⊥AD,
∴BE⊥AD,
∴∠BEO为二面角B-AD-C的平面角,
在Rt△ABC中,BO=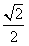 ,AC=
,AC=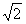 ,
,
∴在Rt△DCA中,AD=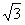 ,∴OE=
,∴OE=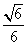 ,
,
∴在Rt△BOE中,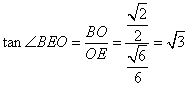 ,∴∠BEO=60°,
,∴∠BEO=60°,
∴二面角B-AD-C的大小为60°。
∴AB⊥BC,
∵AB=BC,
∴∠BCA=∠BAC=45°,
又平面四边形ABCD中,∠C=135°,
∴∠DCA=90°,∴DC⊥AC,
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,DC
 平面ACD,
平面ACD, ∴DC⊥平面ABC,∴AB⊥CD,
∵DC∩BC=C,
∴AB⊥平面BCD,
∵AB
 平面ABD,
平面ABD,∴平面ABD⊥平面PCD。
(Ⅱ)解:设AC的中点为O,连结BO,过O作OE⊥AD于E,连结BE,
∵AB=BC,O为AC的中点,
∴BO⊥AC,
∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,BO
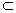 平面ABC,
平面ABC,∴BO⊥平面ACD,
∵OE⊥AD,
∴BE⊥AD,
∴∠BEO为二面角B-AD-C的平面角,
在Rt△ABC中,BO=
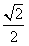 ,AC=
,AC=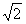 ,
,∴在Rt△DCA中,AD=
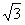 ,∴OE=
,∴OE=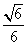 ,
,∴在Rt△BOE中,
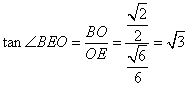 ,∴∠BEO=60°,
,∴∠BEO=60°,∴二面角B-AD-C的大小为60°。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
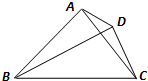 如图,在平面四边形ABCD中,若AB=2,CD=1,则
如图,在平面四边形ABCD中,若AB=2,CD=1,则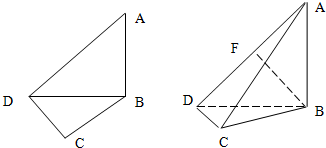 如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.
如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.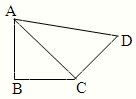 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.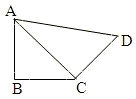 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.