题目内容
设x,y满足约束条件 ,若目标函数z=ax+by,(a>0,b>0)的最大值为12,则
,若目标函数z=ax+by,(a>0,b>0)的最大值为12,则 的最小值为( )
的最小值为( )
 ,若目标函数z=ax+by,(a>0,b>0)的最大值为12,则
,若目标函数z=ax+by,(a>0,b>0)的最大值为12,则 的最小值为( )
的最小值为( )A. | B. | C. | D.4 |
A
解:不等式表示的平面区域如图所示阴影部分,

当直线ax+by=z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6,而 2 /a +3 /b ="(2" /a +3 /b )="2a+3b" /6 ="13" /6 +(b/ a +a/ b )≥13/ 6 +2="25" /6 ,
故2/ a +3/ b 的最小值为:25 /6 .

当直线ax+by=z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6,而 2 /a +3 /b ="(2" /a +3 /b )="2a+3b" /6 ="13" /6 +(b/ a +a/ b )≥13/ 6 +2="25" /6 ,
故2/ a +3/ b 的最小值为:25 /6 .

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 名,女教师
名,女教师 名,
名, 
 和
和 在直线
在直线 的两侧,则
的两侧,则 的取值范围是
的取值范围是 ( )
( ) 或
或
 或
或


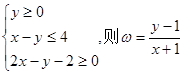 的取值范围是( )
的取值范围是( )



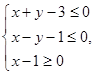 ,O为坐标原点,定点A(6,8),则
,O为坐标原点,定点A(6,8),则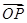 在
在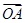 上的投影的范围
上的投影的范围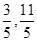 ]
]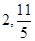 ]
]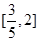
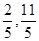 ]
] 满足约束条件
满足约束条件 则
则 的最大值为
的最大值为



 则z=3x-y的最小值为_________.
则z=3x-y的最小值为_________.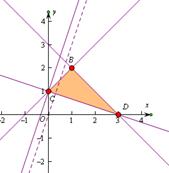
 两个等级.对每种产品,两道工序的加工结果都为
两个等级.对每种产品,两道工序的加工结果都为 级时,产品为一等品,其余均为二等品。
级时,产品为一等品,其余均为二等品。 ;
;


 分别表示一件甲、乙产品的利润,在(1)的条件下,求
分别表示一件甲、乙产品的利润,在(1)的条件下,求 ;
; 名,可用资金
名,可用资金 万元。设
万元。设 分别表示生产甲、乙产品的数量,在(2)的条件下,
分别表示生产甲、乙产品的数量,在(2)的条件下, 最大?最大值是多少?(解答时须给出图示说明)
最大?最大值是多少?(解答时须给出图示说明) 表示的区域面积为 .
表示的区域面积为 .