题目内容
 如图,在矩形ABCD中,AB=2,AD=1,E是CD的中点,以AE为折痕将△DAE向上折起,使D为D′,且平面D′AE⊥平面ABCE.
如图,在矩形ABCD中,AB=2,AD=1,E是CD的中点,以AE为折痕将△DAE向上折起,使D为D′,且平面D′AE⊥平面ABCE.(Ⅰ)求证:AD′⊥EB;
(Ⅱ)求直线AC与平面ABD'所成角的正弦值.
分析:(Ⅰ)根据勾股定理可知AE⊥BE,然后根据面面垂直的性质定理可知BE⊥平面AED',而AD'?平面AED',最后根据线面垂直的性质可知AD'⊥BE;
(Ⅱ)设AC与BE相交于点F,作FG⊥BD',垂足为G,则FG⊥平面ABD',连接AG,则∠FAG是直线AC与平面ABD'所成的角,在Rt△AEF中,求出AF,在Rt△EBD'中,求出FG,最后在三角形FAG求出此角的正弦值即可.
(Ⅱ)设AC与BE相交于点F,作FG⊥BD',垂足为G,则FG⊥平面ABD',连接AG,则∠FAG是直线AC与平面ABD'所成的角,在Rt△AEF中,求出AF,在Rt△EBD'中,求出FG,最后在三角形FAG求出此角的正弦值即可.
解答: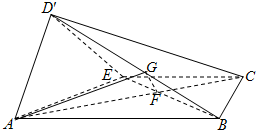 解:(Ⅰ)在Rt△BCE中,BE=
解:(Ⅰ)在Rt△BCE中,BE=
=
,
在Rt△AD'E中,AE=
=
,
∵AB2=22=BE2+AE2,
∴AE⊥BE.(2分)
∵平面AED'⊥平面ABCE,且交线为AE,
∴BE⊥平面AED'.(4分)
∵AD'?平面AED',
∴AD'⊥BE.(6分)
(Ⅱ)设AC与BE相交于点F,由(Ⅰ)知AD'⊥BE,
∵AD'⊥ED',
∴AD'⊥平面EBD',(8分)
∵AD'?平面AED',
∴平面ABD'⊥平面EBD',且交线为BD',
如图,作FG⊥BD',垂足为G,则FG⊥平面ABD',(10分)
连接AG,则∠FAG是直线AC与平面ABD'所成的角.(11分)
由平面几何的知识可知
=
=
,∴EF=
EB=
.
在Rt△AEF中,AF=
=
=
,
在Rt△EBD'中,
=
,可求得FG=
.
∴sin∠FAG=
=
=
.(14分)
∴直线AC与平面ABD'所成的角的正弦值为
.
 解:(Ⅰ)在Rt△BCE中,BE=
解:(Ⅰ)在Rt△BCE中,BE=| BC2+CE2 |
| 2 |
在Rt△AD'E中,AE=
| D′A2+D′E2 |
| 2 |
∵AB2=22=BE2+AE2,
∴AE⊥BE.(2分)
∵平面AED'⊥平面ABCE,且交线为AE,
∴BE⊥平面AED'.(4分)
∵AD'?平面AED',
∴AD'⊥BE.(6分)
(Ⅱ)设AC与BE相交于点F,由(Ⅰ)知AD'⊥BE,
∵AD'⊥ED',
∴AD'⊥平面EBD',(8分)
∵AD'?平面AED',
∴平面ABD'⊥平面EBD',且交线为BD',
如图,作FG⊥BD',垂足为G,则FG⊥平面ABD',(10分)
连接AG,则∠FAG是直线AC与平面ABD'所成的角.(11分)
由平面几何的知识可知
| EF |
| FB |
| EC |
| AB |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 3 |
在Rt△AEF中,AF=
| AE2+EF2 |
2+
|
2
| ||
| 3 |
在Rt△EBD'中,
| FG |
| FB |
| D′E |
| D′B |
2
| ||
| 9 |
∴sin∠FAG=
| FG |
| AF |
| ||||
|
| ||
| 15 |
∴直线AC与平面ABD'所成的角的正弦值为
| ||
| 15 |
点评:本题主要考查线面垂直的性质,以及线面所成角的度量,同时考查空间想象能力,计算能力,转化与化归的思想,解题的关键是寻找线面所成角.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=