题目内容
17.已知三棱锥A-BCD内接与球O,且$BC=BD=CD=2\sqrt{3}$,若三棱锥A-BCD体积的最大值为$4\sqrt{3}$,则球O的表面积为( )| A. | 16π | B. | 25π | C. | 36π | D. | 64π |
分析 确定S△BCD=3$\sqrt{3}$,利用三棱锥A-BCD体积的最大值为$4\sqrt{3}$,可得A到平面BCD的最大距离为4,再利用射影定理,即可求出球的半径,即可求出球O的表面积.
解答 解:∵$BC=BD=CD=2\sqrt{3}$,
∴S△BCD=3$\sqrt{3}$,
∵三棱锥A-BCD体积的最大值为$4\sqrt{3}$,
∴A到平面BCD的最大距离为4,
设球的半径为R,则($\frac{\sqrt{3}}{3}×2\sqrt{3}$)2=4×(2R-4),
∴2R=5,
∴球O的表面积为4πR2=25π.
故选B.
点评 本题考查球的半径,考查表面积的计算,确定A到平面BCD的最大距离为4是关键.

练习册系列答案
相关题目
5.已知点A(-5,0),B(5,0),直线AM,BM的交点为M,AM,BM的斜率之积为$-\frac{16}{25}$,则点M的轨迹方程是( )
| A. | $\frac{x^2}{25}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}-\frac{y^2}{16}=1({x≠±5})$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1({x≠±5})$ |
9.已知偶函数y=f(x)对于任意的$x∈[0,\frac{π}{2})$满足f'(x)cosx+f(x)sinx>0(其中f'(x)是函数f(x)的导函数),则下列不等式中成立的是( )
| A. | $\sqrt{2}f(-\frac{π}{3})<f(\frac{π}{4})$ | B. | $\sqrt{2}f(-\frac{π}{3})<f(-\frac{π}{4})$ | C. | $f(0)>\sqrt{2}f(-\frac{π}{4})$ | D. | $f(\frac{π}{6})<\sqrt{3}f(\frac{π}{3})$ |
6.为了得到函数$y=sin(2x+\frac{π}{3})$的图象,可以将函数$y=sin(2x+\frac{π}{6})$的图象( )
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
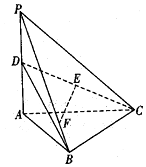 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$. 如图O是等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.
如图O是等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.