题目内容
已知向量 =(1,n),
=(1,n), =(-1,n),若2
=(-1,n),若2 -
- 与
与 垂直,则
垂直,则 在
在 方向上的投影为________.
方向上的投影为________.
1
分析:由两个向量垂直可得他们的数量积等于0,利用两个向量的坐标运算法则,求出这两个向量的坐标,代入数量积公式,解出 n2,从而得到 和
和 .
. 在
在 方向上的投影可用两者的数量积除以
方向上的投影可用两者的数量积除以 的模求出,故需要先求出两者的数量积及
的模求出,故需要先求出两者的数量积及 的模.
的模.
解答:∵向量 ,
, ,
,
∴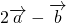 =(3,n),
=(3,n),
∵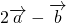 与
与 垂直,
垂直,
∴(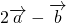 )•
)• =0,
=0,
∴(3,n)•(-1,n)=-3+n2=0,
∴n2=3,
∴ =-1+n2=2,|
=-1+n2=2,| |=2
|=2
∴ 在
在 方向上的投影为
方向上的投影为 =1
=1
故答案为:1.
点评:本题考查平面向量数量积的含义及物理意义,两个向量的数量积公式的应用,两个向量垂直的性质,两个向量坐标形式的运算,本题是概念型题,对概念的熟练掌握与运用对正确解题很重要.
分析:由两个向量垂直可得他们的数量积等于0,利用两个向量的坐标运算法则,求出这两个向量的坐标,代入数量积公式,解出 n2,从而得到
 和
和 .
. 在
在 方向上的投影可用两者的数量积除以
方向上的投影可用两者的数量积除以 的模求出,故需要先求出两者的数量积及
的模求出,故需要先求出两者的数量积及 的模.
的模.解答:∵向量
 ,
, ,
,∴
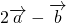 =(3,n),
=(3,n),∵
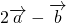 与
与 垂直,
垂直,∴(
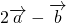 )•
)• =0,
=0,∴(3,n)•(-1,n)=-3+n2=0,
∴n2=3,
∴
 =-1+n2=2,|
=-1+n2=2,| |=2
|=2∴
 在
在 方向上的投影为
方向上的投影为 =1
=1故答案为:1.
点评:本题考查平面向量数量积的含义及物理意义,两个向量的数量积公式的应用,两个向量垂直的性质,两个向量坐标形式的运算,本题是概念型题,对概念的熟练掌握与运用对正确解题很重要.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目