题目内容
（2009•惠州模拟）已知向量
=（1，n），
=（-1，n-2），若
与
共线．则n等于（ ）
| a |
| b |
| a |
| b |
分析：根据向量共线的充要条件的坐标表示式，建立关于n的方程，解之即可得到实数n的值．
解答：解：∵向量
=（1，n），
=（-1，n-2），且
与
共线．
∴1×（n-2）=-1×n，解之得n=1
故选：A
| a |
| b |
| a |
| b |
∴1×（n-2）=-1×n，解之得n=1
故选：A
点评：本题给出向量含有字母n的坐标形式，在已知向量共线的情况下求n的值，着重考查了平面向量共线的充要条件及其坐标表示等知识，属于基础题．
练习册系列答案
相关题目
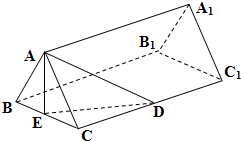（2009•惠州模拟）如图，已知正三棱柱ABC-A1B1C1的底面边长是2，D、E是CC1、BC的中点，AE=DE