题目内容
(文)正数列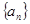 的前
的前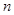 项和
项和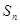 满足:
满足: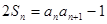 ,
,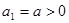
(1)求证: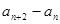 是一个定值;
是一个定值;
(2)若数列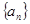 是一个单调递增数列,求
是一个单调递增数列,求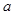 的取值范围;
的取值范围;
(3)若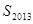 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数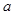 .
.
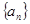 的前
的前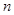 项和
项和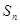 满足:
满足: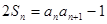 ,
,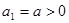
(1)求证:
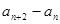 是一个定值;
是一个定值;(2)若数列
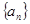 是一个单调递增数列,求
是一个单调递增数列,求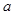 的取值范围;
的取值范围;(3)若
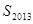 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数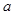 .
.(文)证明:(1) 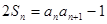 (1)
(1)
 (2)
(2)
 :
:  (3)
(3)
任意 ,
, ,
, 
……………4分
(2)计算
 ……………6分
……………6分
根据数列是隔项成等差,写出数列的前几项:
 ,
, ,
, ,
, ,
, ,。。。。
,。。。。
所以奇数项是递增数列,偶数项是递增数列,整个数列成单调递增的充要条件是
 ……………8分
……………8分
解得 ……………10分
……………10分
(3)


 ……………14分
……………14分
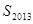 是一个整数,所以
是一个整数,所以 一共4个
一共4个
对一个得1分,合计4分
另解:

 ……………14分
……………14分
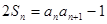 (1)
(1) (2)
(2) :
:  (3)
(3)任意
 ,
, ,
, 
……………4分
(2)计算

 ……………6分
……………6分根据数列是隔项成等差,写出数列的前几项:

 ,
, ,
, ,
, ,
, ,。。。。
,。。。。所以奇数项是递增数列,偶数项是递增数列,整个数列成单调递增的充要条件是
 ……………8分
……………8分解得
 ……………10分
……………10分(3)



 ……………14分
……………14分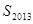 是一个整数,所以
是一个整数,所以 一共4个
一共4个 对一个得1分,合计4分
另解:

 ……………14分
……………14分略

练习册系列答案
相关题目
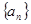 满足:
满足: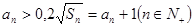 ,其中
,其中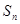 为
为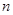 项和。
项和。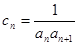 ,
,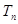 为
为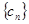 的前
的前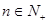 ,不等式
,不等式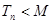 恒成立,求整数
恒成立,求整数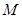 的最小值。
的最小值。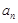 },
},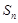 为其前n项的和,
为其前n项的和,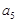 =6,
=6,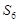 =18,n∈N*.
=18,n∈N*. I)求数列{
I)求数列{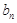 =3
=3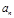 ,求数列{
,求数列{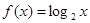 ,若
,若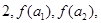
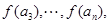
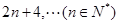 成等差数列.
成等差数列.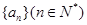 的通项公式;
的通项公式;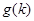 是不等式
是不等式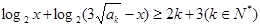 整数解的个数,求
整数解的个数,求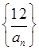 的前n项和为
的前n项和为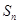 ,是否存在正数
,是否存在正数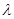 ,对任意正整数
,对任意正整数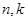 ,使
,使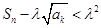 恒成立?若存在,求
恒成立?若存在,求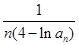 (nÎN*),求数列{bn}的前n项和.
(nÎN*),求数列{bn}的前n项和.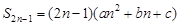 ,则
,则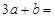 .
. 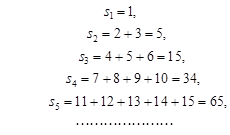
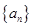 的前
的前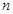 项和为
项和为 ,且
,且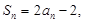 则
则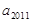 =
=  Sn-1 (n≥2),则Sn=
Sn-1 (n≥2),则Sn=