题目内容
(本小题满分12分)
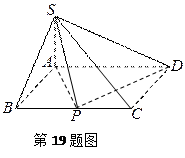
如图,四棱锥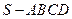 的底面是矩形,
的底面是矩形,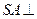 底面
底面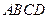 ,
,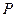 为
为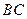 边的中点,
边的中点,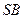 与平面
与平面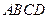 所成的角为45°,且
所成的角为45°,且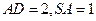 .
.
(Ⅰ)求证: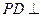 平面
平面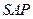 ;
;
(Ⅱ)求二面角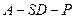 的余弦的大小.
的余弦的大小.

如图,四棱锥
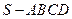 的底面是矩形,
的底面是矩形,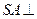 底面
底面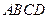 ,
,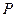 为
为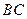 边的中点,
边的中点,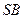 与平面
与平面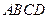 所成的角为45°,且
所成的角为45°,且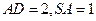 .
.(Ⅰ)求证:
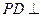 平面
平面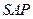 ;
;(Ⅱ)求二面角
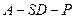 的余弦的大小.
的余弦的大小.解:(Ⅰ)证明:因为 底面
底面 ,
,
所以,∠SBA是SB与平面ABCD所成的角 …………………1分
由已知∠SBA=45°,所以AB=SA=1易求得,AP=PD=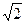 ,…………………
,………………… 3分
3分
又因为AD=2,所以AD2=AP2+PD2,所以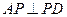 . …………………4分
. …………………4分
因为SA⊥底面ABCD, 平面ABCD,
平面ABCD,
所以SA⊥PD, …………………………………………………………5分
由于S A∩AP=A 所以
A∩AP=A 所以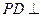 平面SAP.…………………6分
平面SAP.…………………6分
(Ⅱ)设Q为AD的中点,连结PQ ,…………………7分
,…………………7分

由于SA⊥底面ABCD,且SA 平面SAD,
平面SAD,
则平面SAD⊥平面PAD …………………8分
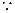
 ,
, PQ⊥平面SAD,
PQ⊥平面SAD,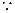 SD
SD 平面SAD,
平面SAD, 
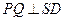 .
.
过Q作QR ,垂足为
,垂足为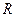 ,连接
,连接 ,则
,则 .
.
又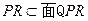 ,
, ,
,

 ∠PRQ是二面角A-SD-P的平面角.…………10分
∠PRQ是二面角A-SD-P的平面角.…………10分
容易证明△DRQ∽△D AS,则
AS,则 .
.
因为 ,
,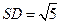 ,
,
所以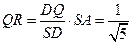 . …………………12分
. …………………12分
在Rt△PRQ中,因为PQ=AB=1,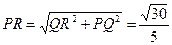 ,
,
所以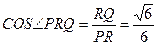 . …………………13分
. …………………13分
所以二面角A-SD-P的余弦为 .…………………14分
.…………………14分
解法二:因为 底面
底面 ,
,
所以,∠SBA是SB与平面ABCD所成的角. ……1分
由已知∠SBA=45° ,所以AB=SA=1
,所以AB=SA=1
建立空间直角坐标系(如图)

 由已知,P为BC中点.
由已知,P为BC中点.
于是A(0,0,0)、B(1,0,0)、P(1,1,0)、D(0,2,0)、S(0,0,1)……………3分
(Ⅰ)易求得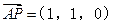 ,
,
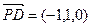 ,
, .……………
.…………… ……4分
……4分
因为 ,
, .
.
所以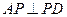 ,
, .
.
由于 ,所以
,所以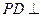 平面
平面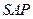
 . …………………6分
. …………………6分
(Ⅱ)设平面SPD的 法向量为
法向量为 .
.
由 ,得
,得 解得
解得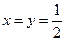 ,
,
所以 . …………………9分
. …………………9分
又因为AB⊥平面SAD,所以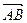 是平面SAD的法向量,
是平面SAD的法向量,
易得 .…………………9分
.…………………9分
所以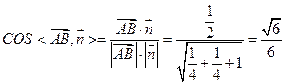 . …………………13分
. …………………13分
所以所求二面角 的余弦值为
的余弦值为 .…………………14分
.…………………14分
 底面
底面 ,
,所以,∠SBA是SB与平面ABCD所成的角 …………………1分
由已知∠SBA=45°,所以AB=SA=1易求得,AP=PD=
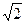 ,…………………
,………………… 3分
3分又因为AD=2,所以AD2=AP2+PD2,所以
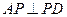 . …………………4分
. …………………4分因为SA⊥底面ABCD,
 平面ABCD,
平面ABCD,所以SA⊥PD, …………………………………………………………5分
由于S
 A∩AP=A 所以
A∩AP=A 所以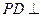 平面SAP.…………………6分
平面SAP.…………………6分(Ⅱ)设Q为AD的中点,连结PQ
 ,…………………7分
,…………………7分
由于SA⊥底面ABCD,且SA
 平面SAD,
平面SAD,则平面SAD⊥平面PAD …………………8分
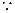
 ,
, PQ⊥平面SAD,
PQ⊥平面SAD,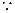 SD
SD 平面SAD,
平面SAD, 
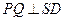 .
.过Q作QR
 ,垂足为
,垂足为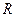 ,连接
,连接 ,则
,则 .
.又
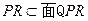 ,
, ,
,
 ∠PRQ是二面角A-SD-P的平面角.…………10分
∠PRQ是二面角A-SD-P的平面角.…………10分容易证明△DRQ∽△D
 AS,则
AS,则 .
.因为
 ,
,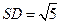 ,
,所以
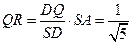 . …………………12分
. …………………12分在Rt△PRQ中,因为PQ=AB=1,
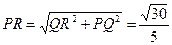 ,
,所以
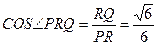 . …………………13分
. …………………13分所以二面角A-SD-P的余弦为
 .…………………14分
.…………………14分解法二:因为
 底面
底面 ,
,所以,∠SBA是SB与平面ABCD所成的角. ……1分
由已知∠SBA=45°
 ,所以AB=SA=1
,所以AB=SA=1建立空间直角坐标系(如图)

 由已知,P为BC中点.
由已知,P为BC中点.于是A(0,0,0)、B(1,0,0)、P(1,1,0)、D(0,2,0)、S(0,0,1)……………3分
(Ⅰ)易求得
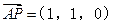 ,
,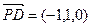 ,
, .……………
.…………… ……4分
……4分因为
 ,
, .
.所以
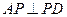 ,
, .
.由于
 ,所以
,所以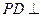 平面
平面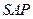
 . …………………6分
. …………………6分(Ⅱ)设平面SPD的
 法向量为
法向量为 .
.由
 ,得
,得 解得
解得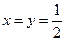 ,
,所以
 . …………………9分
. …………………9分又因为AB⊥平面SAD,所以
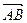 是平面SAD的法向量,
是平面SAD的法向量,易得
 .…………………9分
.…………………9分所以
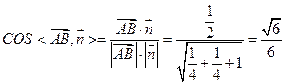 . …………………13分
. …………………13分所以所求二面角
 的余弦值为
的余弦值为 .…………………14分
.…………………14分略

练习册系列答案
相关题目
 的边长为4,
的边长为4,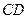 是
是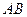 边上的高,
边上的高,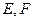 分别是
分别是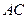 和
和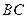 边的中点,现将△
边的中点,现将△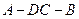 .
.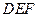 的位置关系,并
的位置关系,并 说明理由;
说明理由;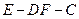 的余弦值;
的余弦值;
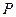 ,使
,使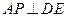 ?证明你的结论.
?证明你的结论. 
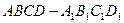 中,
中,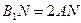 ,
,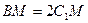
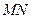 的长度。(12分)
的长度。(12分)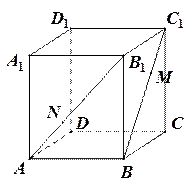
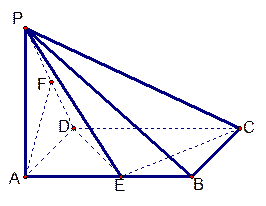
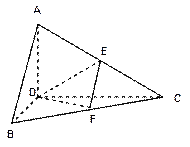
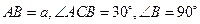 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角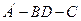 的大小记为
的大小记为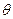 .
.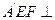 平面BCD;
平面BCD; 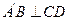 时,求
时,求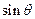 的值;
的值; 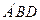 的距离.
的距离.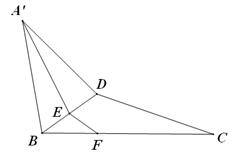
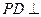 平面
平面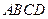 ,
,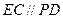 ,
,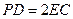 ,
, 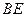 //平面
//平面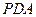 ;
;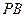 的中点,求证:
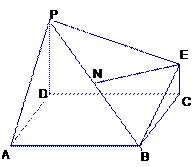
的中点,求证: 平面
平面 ;
;
 的球面上三点,且A
的球面上三点,且A B=2,BC=4,
B=2,BC=4,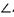 ABC=
ABC=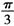 为球心,则二面角0-AB-C的大小为( )
为球心,则二面角0-AB-C的大小为( )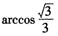 B.
B.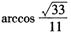 C.
C.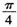 D.
D.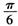
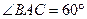 ,D为BC的中点。
,D为BC的中点。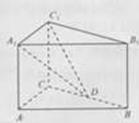
 1—C的大小。
1—C的大小。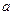 平行于平面
平行于平面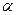 ,直线
,直线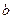 在平面
在平面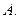 平行
平行  异面
异面  平行或异面
平行或异面  平行、相交或异面
平行、相交或异面