题目内容
如图5,![]() 中,
中,![]() 点
点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]()
(Ⅰ)求![]() 的长;
的长;
(Ⅱ)求![]() 的面积.
的面积.
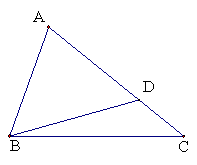 |
|
解:(Ⅰ)因为![]() ,所以
,所以![]() .······················ 2分
.······················ 2分
在![]() 中,设
中,设![]() ,
,
则由余弦定理可得![]() ①························································ 5分
①························································ 5分
在![]() 和
和![]() 中,由余弦定理可得
中,由余弦定理可得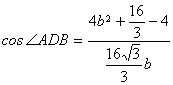 ,
,
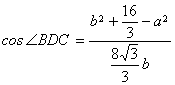 .··········································································· 7分
.··········································································· 7分
因为![]() ,
,
所以有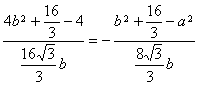 ,所以3
,所以3![]() =-6 ②
=-6 ②
由①②可得![]() ,即
,即![]() .································································ 9分
.································································ 9分
(Ⅱ)由(Ⅰ)得![]() 的面积为
的面积为![]() ,
,
所以![]() 的面积为
的面积为![]() .········································································· 12分
.········································································· 12分
(注:也可以设![]() ,所以
,所以![]() ,用向量法解决;或者以
,用向量法解决;或者以![]() 为
为
原点,![]() 为
为![]() 轴建立平面直角坐标系,用坐标法解答;或者过
轴建立平面直角坐标系,用坐标法解答;或者过![]() 作
作![]() 平行线交
平行线交![]() 延长线于
延长线于![]() ,用正余弦定理解答.具体过程略)
,用正余弦定理解答.具体过程略)

练习册系列答案
相关题目
 中,
中,
 在线段
在线段 上,且
上,且 ,
,
 的长;
的长; 的面积.
的面积.
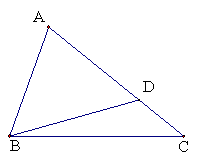 如图5,
如图5,