题目内容
在等比数列{an}中，满足a2+a3+a4=28，a3+2是a2、a4的等差中项，且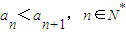
．（Ⅰ）求数列{an}的通项公式；
（Ⅱ）记
，求数列{bn}的前n项和为Tn．
【答案】分析：（Ⅰ）利用a2+a3+a4=28，a3+2是a2、a4的等差中项，an＜an+1，求出首项与公比，即可求数列{an}的通项公式；
（Ⅱ）由
，确定通项，利用错位相减法，可求数列{bn}的前n项和为Tn．
解答：解：（Ⅰ）设数列{an}的公比为q，由a2+a3+a4=28，a2+a4=2（a3+2），an＜an+1得a1=2，q=2．…（4分）
∴数列{an}的通项公式为
．…（6分）
（Ⅱ）∵
，
，①
∴
．②
①-②得：
…（12分）
∴
，…（14分）
点评：本题考查数列的通项与求和，考查错位相减法的运用，考查学生的计算能力，属于中档题．
（Ⅱ）由
，确定通项，利用错位相减法，可求数列{bn}的前n项和为Tn．解答：解：（Ⅰ）设数列{an}的公比为q，由a2+a3+a4=28，a2+a4=2（a3+2），an＜an+1得a1=2，q=2．…（4分）
∴数列{an}的通项公式为
．…（6分）（Ⅱ）∵
，，①∴
．②①-②得：
…（12分）∴
，…（14分）点评：本题考查数列的通项与求和，考查错位相减法的运用，考查学生的计算能力，属于中档题．
练习册系列答案
53随堂测系列答案
相关题目
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（ ）
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|