题目内容
函数f(x)在定义域R内可导,若f(x)=f(4-x),且当x∈(-∞,2)时,(x-2)·f′(x)<0,设a=f(4),b=f(1), c=f(-1),则a,b,c由小到大排列为 ( )
| A.a<b<c | B.a<c<b | C.c<b<a | D.c<a<b |
D
解析试题分析:根据题意,由于f(x)=f(4-x),说明函数关于x=2对称,且当x∈(-∞,2)时,(x-2)·f′(x)<0,则说明函数递增,在x>2时,函数递减,那么可知,2-(-1)>4-2,则根据函数对称性可知,函数值的大小关系为c<a<b,选D.
考点:函数单调性
点评:主要是考查了导数与函数单调性的关系的运用,属于基础题。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
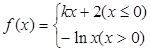 ,则下列关于
,则下列关于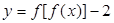 的零点个数判断正确的是( )
的零点个数判断正确的是( )
| A.当k=0时,有无数个零点 | B.当k<0时,有3个零点 |
| C.当k>0时,有3个零点 | D.无论k取何值,都有4个零点 |
已知函数 的值域为
的值域为 ,函数
,函数 的定义域为
的定义域为 ,则
,则
A. | B. | C. | D. |
已知函数 是
是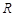 上的奇函数.当
上的奇函数.当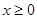 时,
时, ,则
,则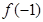 的值是 ( )
的值是 ( )
| A.3 | B.-3 | C.-1 | D.1 |
若定义在R上的偶函数 满足
满足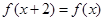 ,且当
,且当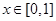 时,
时,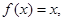 则方程
则方程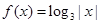 的解个数是( )
的解个数是( )
| A.0个 | B.2个 | C.4个 | D.6个 |
函数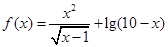 的定义域为( )
的定义域为( )
| A.R | B.[1,10] | C.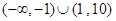 | D.(1,10) |
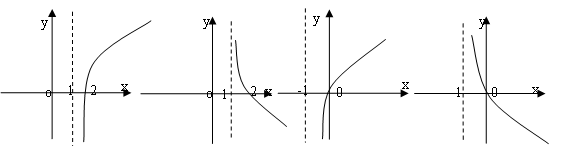
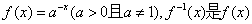 的反函数,若
的反函数,若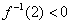 ,则
,则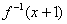 的图象大致是( )
的图象大致是( )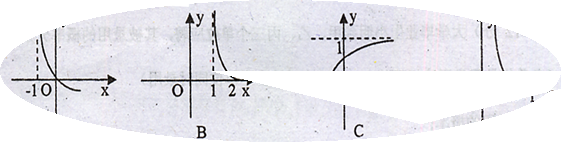
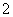 的等边三角形
的等边三角形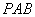 沿
沿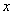 轴滚动,某时刻
轴滚动,某时刻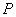 与坐标原点重合(如图),设顶点
与坐标原点重合(如图),设顶点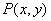 的轨迹方程是
的轨迹方程是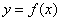 ,关于函数
,关于函数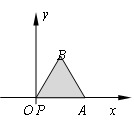
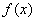 的值域为
的值域为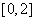 ;
;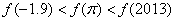 ;
;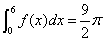 .
.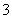
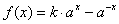 (
( 且
且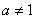 )在
)在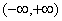 上既是奇函数又是增函数,则
上既是奇函数又是增函数,则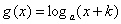 的图象是
的图象是