题目内容
函数y=sin(-2x)的单调递增区间是________.
[kπ+ ,kπ+
,kπ+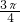 ],k∈Z
],k∈Z
分析:先把所求问题转化为求t=sin2x的单调递减区间,再借助于正弦函数的单调性即可得到答案.
解答:y=sin(-2x)=-sin2x.
所以即为求t=sin2x的单调递减区间,
∴2kπ ≤2x≤2kπ+
≤2x≤2kπ+ ?kπ+
?kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
故答案为:[kπ+ ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
点评:本题主要考查正弦函数的单调性.解决此类问题一般都要用到整体代入思想.
 ,kπ+
,kπ+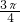 ],k∈Z
],k∈Z分析:先把所求问题转化为求t=sin2x的单调递减区间,再借助于正弦函数的单调性即可得到答案.
解答:y=sin(-2x)=-sin2x.
所以即为求t=sin2x的单调递减区间,
∴2kπ
 ≤2x≤2kπ+
≤2x≤2kπ+ ?kπ+
?kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.故答案为:[kπ+
 ,kπ+
,kπ+ ],k∈Z.
],k∈Z.点评:本题主要考查正弦函数的单调性.解决此类问题一般都要用到整体代入思想.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目