题目内容
设函数 ,
, ,
, 为常数
为常数
(1)求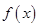 的最小值
的最小值 的解析式;
的解析式;
(2)在(1)中,是否存在最小的整数 ,使得
,使得 对于任意
对于任意 均成立,若存在,求出
均成立,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据二次函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,又函数
上单调递增,又函数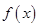 的对称轴为直线
的对称轴为直线 ,且
,且 ,可分
,可分 ,
, ,
,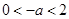 进行分类讨论,从而求得函数
进行分类讨论,从而求得函数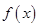 的最小值
的最小值 的解析式;(2)由(1)知当
的解析式;(2)由(1)知当 时,函数
时,函数 为单调递减函数,且最大值为
为单调递减函数,且最大值为 ,当
,当 时,函数
时,函数 ,在
,在 上为单调递增,在
上为单调递增,在 上单调递减,最大值为
上单调递减,最大值为 ,当
,当 时,函数
时,函数 为单调递增,最大值为
为单调递增,最大值为 ,所以关于自变量
,所以关于自变量 的函数
的函数 的最大值为
的最大值为 ,又由不等式
,又由不等式 得
得 ,对于任意
,对于任意 均成立,从而存在最小的整数
均成立,从而存在最小的整数 .
.
试题解析:(1)由题意,函数 图像是开口向上,对称轴
图像是开口向上,对称轴 的抛物线,
的抛物线,
当 时,
时,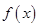 在
在 上是增函数,
上是增函数, 时有最小值
时有最小值
当 时,
时,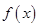 在
在 上是减函数,
上是减函数, 时有最小值
时有最小值
③当 时,
时,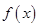 在
在 上是不单调,
上是不单调, 时有最小值
时有最小值
 8分
8分
(2)存在,由题知 在
在 是增函数,在
是增函数,在 是减函数
是减函数 时,
时, ,
, 恒成立
恒成立 ,
,
 为整数,
为整数, 的最小值为
的最小值为 14分
14分
考点:二次函数单调性、最值.

练习册系列答案
相关题目
 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 ,
, .
.  为奇函数,求实数
为奇函数,求实数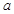 的值;
的值; 上的所有上界构成的集合;
上的所有上界构成的集合; 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 (
( 为实常数).
为实常数). 图像上动点
图像上动点 到定点
到定点 的距离的最小值为
的距离的最小值为 ,求实数
,求实数 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数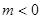 ,若不等式
,若不等式 在
在 有解,求
有解,求 的取值范围.
的取值范围. ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元. 是定义在(-1,1)上的奇函数,其中
是定义在(-1,1)上的奇函数,其中 ,a为正整数,且满足
,a为正整数,且满足 .
. 的解析式;
的解析式; 的
的 的范围;
的范围; .
.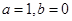 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数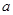 的取值范围.
的取值范围. 同时满足以下三个条件时称
同时满足以下三个条件时称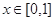 ,总有
,总有 ;
; 成立,则下列判断正确的有 .
成立,则下列判断正确的有 . ;
; 在区间[0,1]上是“友谊函数”;
在区间[0,1]上是“友谊函数”; <
< ≤1,则
≤1,则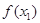 ≤
≤ .
.  上的函数
上的函数 ,若存在闭区间
,若存在闭区间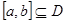 和常数
和常数 ,使得对任意的
,使得对任意的 ,都有
,都有 ,且对任意的
,且对任意的 都有
都有 恒成立,则称函数
恒成立,则称函数 型”函数.
型”函数. 是
是 上的“
上的“ 对一切的
对一切的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是区间
是区间 上的“
上的“ 和
和 的值.
的值. 的函数
的函数 是奇函数.
是奇函数. 的值
的值 的单调性;
的单调性; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.