题目内容
已知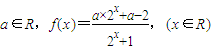
(1)确定a的值,使f(x)为奇函数.
(2)在(1)的条件下,试问K为何值时方程f-1(x)=log2K有正根?
【答案】分析:(1)根据 f(0)=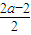 =0,求得 a的值.
=0,求得 a的值.
(2)在(1)的条件下,f(x)=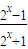 =1-
=1-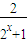 ,求得 f-1(x)=
,求得 f-1(x)=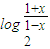 ,由题意知方程
,由题意知方程 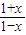 =k 在k>0时 有正根,故有k>0 且 x=
=k 在k>0时 有正根,故有k>0 且 x=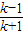 >0,解得 k 的值.
>0,解得 k 的值.
解答:解:(1)若f(x)为奇函数时,则应有 f(0)=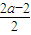 =0,∴a=1.
=0,∴a=1.
故当a=1时,f(x)为奇函数.
(2)在(1)的条件下,f(x)=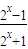 =1-
=1-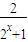 ,
,
∴2x= -1,x=
-1,x=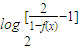 ,∴f-1(x)=
,∴f-1(x)=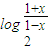 .
.
方程f-1(x)=log2K有正根,即.
∴k>0 且 x=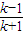 >0,解得 k>1.
>0,解得 k>1.
故当k>1 时,方程f-1(x)=log2K有正根.
点评:本题考查函数的奇偶性的判断,求反函数,体现了转化的数学思想,得到 k>0 且 x=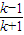 >0,是解题的
>0,是解题的
关键.
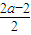 =0,求得 a的值.
=0,求得 a的值.(2)在(1)的条件下,f(x)=
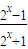 =1-
=1-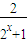 ,求得 f-1(x)=
,求得 f-1(x)=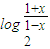 ,由题意知方程
,由题意知方程 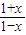 =k 在k>0时 有正根,故有k>0 且 x=
=k 在k>0时 有正根,故有k>0 且 x=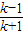 >0,解得 k 的值.
>0,解得 k 的值.解答:解:(1)若f(x)为奇函数时,则应有 f(0)=
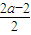 =0,∴a=1.
=0,∴a=1.故当a=1时,f(x)为奇函数.
(2)在(1)的条件下,f(x)=
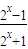 =1-
=1-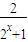 ,
,∴2x=
 -1,x=
-1,x=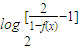 ,∴f-1(x)=
,∴f-1(x)=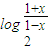 .
.方程f-1(x)=log2K有正根,即.
∴k>0 且 x=
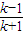 >0,解得 k>1.
>0,解得 k>1.故当k>1 时,方程f-1(x)=log2K有正根.
点评:本题考查函数的奇偶性的判断,求反函数,体现了转化的数学思想,得到 k>0 且 x=
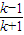 >0,是解题的
>0,是解题的关键.

练习册系列答案
相关题目
