题目内容
已知函数f(x)=2 cos2x+sin2x-
cos2x+sin2x- +1(x∈R).
+1(x∈R).
(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)若x∈[- ,
, ],求f(x)的值域.
],求f(x)的值域.
 cos2x+sin2x-
cos2x+sin2x- +1(x∈R).
+1(x∈R).(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)若x∈[-
 ,
, ],求f(x)的值域.
],求f(x)的值域.(1)π
(2)f(x)的单调递增区间为[kπ- ,kπ+
,kπ+ ](k∈Z)
](k∈Z)
(3)f(x)∈[0,3]
(2)f(x)的单调递增区间为[kπ-
 ,kπ+
,kπ+ ](k∈Z)
](k∈Z)(3)f(x)∈[0,3]
解:f(x)=sin2x+ (2cos2x-1)+1=sin2x+
(2cos2x-1)+1=sin2x+ cos2x+1=2sin(2x+
cos2x+1=2sin(2x+ )+1.
)+1.
(1)函数f(x)的最小正周期为T= =π.
=π.
(2)由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ (k∈Z),
(k∈Z),
得2kπ- ≤2x≤2kπ+
≤2x≤2kπ+ (k∈Z).
(k∈Z).
∴kπ- ≤x≤kπ+
≤x≤kπ+ (k∈Z).
(k∈Z).
∴函数f(x)的单调递增区间为[kπ- ,kπ+
,kπ+ ](k∈Z).
](k∈Z).
(3)∵x∈[- ,
, ],
],
∴2x+ ∈[-
∈[- ,
, ].
].
∴sin(2x+ )∈[-
)∈[- ,1].
,1].
∴f(x)∈[0,3].
 (2cos2x-1)+1=sin2x+
(2cos2x-1)+1=sin2x+ cos2x+1=2sin(2x+
cos2x+1=2sin(2x+ )+1.
)+1.(1)函数f(x)的最小正周期为T=
 =π.
=π.(2)由2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ (k∈Z),
(k∈Z),得2kπ-
 ≤2x≤2kπ+
≤2x≤2kπ+ (k∈Z).
(k∈Z).∴kπ-
 ≤x≤kπ+
≤x≤kπ+ (k∈Z).
(k∈Z).∴函数f(x)的单调递增区间为[kπ-
 ,kπ+
,kπ+ ](k∈Z).
](k∈Z).(3)∵x∈[-
 ,
, ],
],∴2x+
 ∈[-
∈[- ,
, ].
].∴sin(2x+
 )∈[-
)∈[- ,1].
,1].∴f(x)∈[0,3].

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
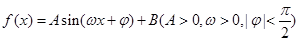 在某一
在某一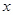














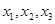 ,并直接写出函数
,并直接写出函数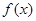 的解析式;
的解析式;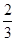 个单位得到函数
个单位得到函数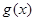 ,若函数
,若函数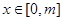 (其中
(其中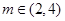 )上的值域为
)上的值域为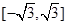 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为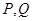 ,求
,求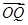 与
与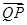 夹角
夹角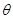 的大小.
的大小. )的图象,只需要将函数y=3cos2x的图象( )
)的图象,只需要将函数y=3cos2x的图象( ) 个单位
个单位 个单位
个单位 的图像关于直线
的图像关于直线 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 .
. 和
和 的值;
的值; ,求
,求 的值.
的值.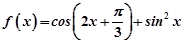 .
.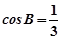 ,
,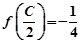 ,且C为锐角,求
,且C为锐角,求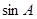 .
.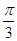 )(ω>0)的单调递增区间为[kπ-
)(ω>0)的单调递增区间为[kπ-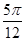 ,kπ+
,kπ+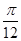 ](k∈Z),单调递减区间为[kπ+
](k∈Z),单调递减区间为[kπ+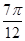 ](k∈Z),则ω的值为________.
](k∈Z),则ω的值为________. .
.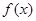 的值域;
的值域; 的内角
的内角 的对边长分别为
的对边长分别为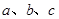 ,若
,若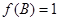 ,
,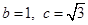 ,求
,求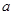 的值.
的值. 直线
直线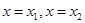 是
是 图像的任意两条对称轴,且
图像的任意两条对称轴,且 的最小值为
的最小值为 .
. 的单调增区间;
的单调增区间; 的
的 的取值范围.
的取值范围. 求
求 的值;
的值;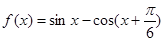 的值域为
的值域为