题目内容
已知椭圆![]() :
:![]() 的面积为π
的面积为π![]() ,
,![]() 包含于平面区域
包含于平面区域![]()
 内,向平面区域
内,向平面区域![]() 内随机投一点Q,点Q落在椭圆内的概率为
内随机投一点Q,点Q落在椭圆内的概率为![]() .
.
(Ⅰ)试求椭圆![]() 的方程;
的方程;
![]() (Ⅱ)若斜率为
(Ⅱ)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一点,
上一点,
记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,试问:
,试问:![]() 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() 为定值0
为定值0
解析:
(Ⅰ)平面区域![]()
 是一个矩形区域,如图所示. ………2分
是一个矩形区域,如图所示. ………2分
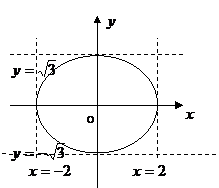
依题意及几何概型,可得![]() , ……………………3分
, ……………………3分
即 ![]() . 因为
. 因为 ![]() ,
,
所以, ![]() .
.
………………5分
所以,椭圆![]() 的方程为
的方程为![]() ……6分
……6分
(Ⅱ)设直线![]() 的方程为:
的方程为:![]() ,
,![]()
联立直线![]() 的方程与椭圆方程得:
的方程与椭圆方程得:
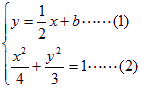
(1)代入(2)得:![]()
化简得:![]() ………(3) ……………8分
………(3) ……………8分
当![]() 时,即,
时,即,![]()
也即,![]() 时,直线
时,直线![]() 与椭圆有两交点,
与椭圆有两交点,
由韦达定理得: , ………………10分
, ………………10分
所以, ,
, 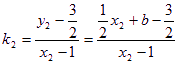
![]() 则
则![]()
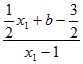
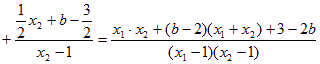
![]() ……………13分
……………13分
所以,![]() 为定值。 ……………14分
为定值。 ……………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•闵行区一模)已知椭圆E的方程为
(2013•闵行区一模)已知椭圆E的方程为