题目内容
【题目】已知函数![]() .
.
(1)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据![]() 是偶函数,可得
是偶函数,可得![]() ,利用恒等,即可求出结果;
,利用恒等,即可求出结果;
(2)当![]() 时,
时,![]() 有且只有一实根,可得
有且只有一实根,可得![]() ,然后再利用换元法,设
,然后再利用换元法,设![]() ,
,![]() ,转化为
,转化为![]() ,
,![]() 有一实根,根据根的分布,即可求出结果;
有一实根,根据根的分布,即可求出结果;
(3)设![]() ,对分段函数的零点分析可得
,对分段函数的零点分析可得![]() ,即
,即![]() ,
,![]() ,消除
,消除![]() ,整理可得
,整理可得![]() ,进而可得
,进而可得![]() ,据此即可求证结果.
,据此即可求证结果.
(1)![]() 是偶函数,所以
是偶函数,所以![]() ,则
,则![]() .
.
所以![]() .
.
(2)当![]() 时,
时,![]() 有且只有一实根,即
有且只有一实根,即![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() 有一实根,
有一实根,
∵![]() 恒成立,两根之积小于0,所以
恒成立,两根之积小于0,所以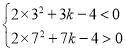 ,
,
∴![]() .
.
(3)不妨设![]() ,则
,则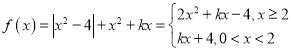 ,
,
若![]() ,与
,与![]() 矛盾,
矛盾,
若![]() ,与
,与![]() 是单调函数矛盾,
是单调函数矛盾,
所以![]() ;
;
所以![]() ①,
①,![]() ②,
②,
由①,得:![]() ,由②,得:
,由②,得:![]() ;
;
联立①、②消去![]() 得:
得:![]() ,即
,即![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .
.

练习册系列答案
相关题目