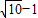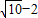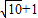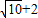题目内容
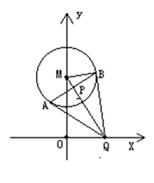
已知⊙M：
轴上的动点，QA，QB分别切⊙M于A，B两点，（1）如果
，求直线MQ的方程；
（2）求动弦AB的中点P的轨迹方程.
（1）直线AB方程是
（2）
解析:
（1）由
，可得
由射影定理，得 
在Rt△MOQ中，
，
故
，
所以直线AB方程是
（2）连接MB，MQ，设
由
点M，P，Q在一直线上，得
由射影定理得
即
把（*）及（**）消去a，
并注意到
，可得
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知抛物线x2=4y上的动点P在x轴上的射影为点M，点A（3，2），则|PA|+|PM|的最小值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
上的动点，点P在x轴上的射影为M，点A的坐标是
，则|PA|+|PM|的最小值是（ ）
