题目内容

若等腰梯形ABCD中，AB∥CD，AB=3，BC=
2
，∠ABC=45°，则
AB
•
CD
的值为（　　）
分析：利用两个向量的加减法的法则，以及其几何意义，化简
AB
•
CD
 为
AB
•（
CB
+
BA
+
AD
）=
AB
•
CB
+
AB
•
BA
+
AB
•
AD
，再利用两个向量的数量积的定义求得结果．
解答：解：由题意可得，AD=BC=
2
，∠BAD=∠ABC=45°．
则由
AB
•
CD
=
AB
•（
CB
+
BA
+
AD
）=
AB
•
CB
+
AB
•
BA
+
AB
•
AD
=3×
2
×cosB-
AB
2+3×
2
×cos45°=3-9+3=-3，
故选A．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，属于中档题．
练习册系列答案
相关题目
若等腰梯形ABCD中，AB∥CD，AB=3，BC=
2
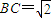，∠ABC=45°，则
AC
•
BD
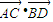的值为（　　）

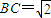若等腰梯形ABCD中，AB∥CD，AB＝3，BC＝，∠ABC＝45°，则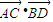·的值为

[　　]
A．

－3

B．

－7

C．

3

D．

9
若等腰梯形ABCD中，AB∥CD，AB=3，，∠ABC=45°，则的值为（ ）
A．-3
B．-7
C．3
D．9
若等腰梯形ABCD中，AB∥CD，AB=3，，∠ABC=45°，则的值为（ ）
A．-3
B．-7
C．3
D．9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网