题目内容
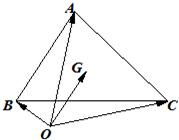
如图，⊙O是△ABC的外接圆，延长BC边上的高AD交⊙O于点E，H为△ABC的垂心．求证：DH=DE．分析：连接CE，CH，结合H为△ABC的垂心可得∠ECD=∠HCD，进而得△HDC≌△EDC即可得到结论．
解答：证明：连接CE，CH，因为H为△ABC的垂心；
CH⊥AB
所以：∠ECD=∠BAD=90°-∠ABC，∠HCD=90°-∠ABC，
从而∠ECD=∠HCD．
又因为CD⊥HE，CD为公共边，
所以△HDC≌△EDC，
所以：DH=DE．
CH⊥AB
所以：∠ECD=∠BAD=90°-∠ABC，∠HCD=90°-∠ABC，
从而∠ECD=∠HCD．
又因为CD⊥HE，CD为公共边，
所以△HDC≌△EDC，
所以：DH=DE．
点评：本题主要考察圆內接多边形的性质与判定以及三角形全等的证明．解决本题的关键在于能根据H为△ABC的垂心得∠ECD=∠HCD．
练习册系列答案
相关题目
（2012•丹东模拟）如图，⊙O是△ABC的外接圆，D是弧AC的中点，BD交AC于E．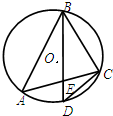 
（2011•丹东模拟）选修4-1：几何证明选讲
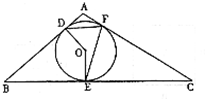如图，⊙O是△ABC的内切圆，切点分别是D、E、F，已知∠A=100°，∠C=30°，则∠DFE的度数是（ ）