在平面α内有直径为AB的⊙O,若SA⊥α且使∠SBA=30°,在⊙O上的点M使∠MAB=θ,又知点A在SB.SM上的射影P.Q使∠APQ=φ,如右图所示.求证:(1)SB⊥平面APQ;(2)tanθ·tanφ=2. 题目和参考答案——青夏教育精英家教网—

题目内容

在平面α内有直径为AB的⊙O,若SA⊥α且使∠SBA=30°,在⊙O上的点M使∠MAB=θ,又知点A在SB、SM上的射影P、Q使∠APQ=φ,如右图所示.求证: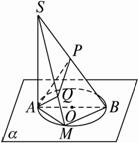

(1)SB⊥平面APQ;

(2)tanθ·tanφ=2.

试题答案

相关练习册答案

证明:(1)∵AQ在α内的射影AM⊥BMAQ⊥BM.

又AQ⊥SM,

∴AQ⊥面SBMAQ⊥PQ,AQ⊥SB.

∴SB⊥面APQ.

(2)∵AM⊥BM,AQ⊥PQ,

∴tanθ=,tanφ=.

∵Rt△SPQ∽Rt△SMB,

∴PQ=.

又∵在Rt△SAM中,AQ=,

∴tanφ=.

∴tanθ·tanφ=.

∵在Rt△SPA中,=csc30°,

∴tanθ·tanφ=2.

练习册系列答案

大爱图书纵向解析与命题设计中考试题精选系列答案

首师金卷重点校中考模拟测试卷系列答案

赢在起跑线快乐寒假河北少年儿童出版社系列答案

春雨教育考必胜中考试卷精选系列答案

天利38套解锁中考真题档案系列答案

相关题目

如图，已知二面角α-l-β的平面角为45°，在半平面α内有一个半圆O，其直径AB在l上，M是这个半圆O上任一点（除A、B外），直线AM、BM与另一个半平面β所成的角分别为θ₁、θ₂．试证明cos²θ₁+cos²θ₂为定值．

如图所示，平面α内有一以AB为直径的圆，PA⊥α,点C在圆周上动（不与A、B重合），点D、E分别是A在PC、PB上的射影，下面结论:

①∠AED是二面角A—PB—C的平面角;

②∠ACD是二面角P—BC—A的平面角;

③∠EDA是二面角A—PC—B的平面角;

④∠BAC是二面角B—PA—C的平面角;

⑤∠PAC是二面角P—AB—C的平面角.

其中正确结论的序号是____________________.

如图所示,平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A、B重合),点D、E分别是A在PC、PB上的射影.有下面结论：
①∠AED是二面角A-PB-C的平面角；
②∠ACD是二面角P-BC-A的平面角；
③∠EDA是二面角A-PC-B的平面角；
④∠BAC是二面角B-PA-C的平面角；
⑤∠PAC是二面角P-AB-C的平面角.
其中正确结论的序号是__________.

（本小题满分12分）

有编号为,,…的10个零件，测量其直径（单位：cm），得到下面数据：

其中直径在区间[1.48，1.52]内的零件为一等品。

（Ⅰ）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

（Ⅱ）从一等品零件中，随机抽取2个.

     （ⅰ）用零件的编号列出所有可能的抽取结果；

     （ⅱ）求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分

【解析】（Ⅰ）解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P（A）==.

      （Ⅱ）（i）解：一等品零件的编号为.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,

,,,共有15种.

      (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”（记为事件B）的所有可能结果有：，，共有6种.

      所以P(B)=.

（本小题满分12分）

如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=，∠BAD＝∠CDA＝45°.

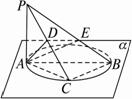
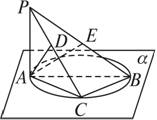
（Ⅰ）求异面直线CE与AF所成角的余弦值；

（Ⅱ）证明CD⊥平面ABF；