题目内容
如图,在直角坐标系其对角线![]() 依次放置在
依次放置在![]() 轴上(相邻顶点重合).设
轴上(相邻顶点重合).设![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,点
的等差数列,点![]() 的坐标为
的坐标为![]() .
.
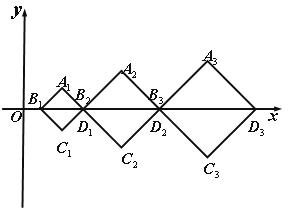
(1)当![]() 时,证明:顶点
时,证明:顶点![]() 不在同一条直线上;
不在同一条直线上;
(2)在(1)的条件下,证明:所有顶点![]() 均落在抛物线
均落在抛物线![]() 上;
上;
(3)为使所有顶点![]() 均落在抛物线
均落在抛物线![]() 上,求
上,求![]() 与
与![]() 之间所应满足的关系式.
之间所应满足的关系式.
解答:本题主要考查直线方程、直线和抛物线的位置关系以及数列的综合问题.
[证明](1)由题意可知,![]() ,
,
∴![]()
![]() ,
,
∴顶点![]() 不在同一条直线上
不在同一条直线上
(2)由题意可知,顶点![]() 的横坐标
的横坐标![]()
![]() ,
,
顶点![]() 的纵坐标
的纵坐标![]()
∵对任意正整数![]() ,点
,点![]()
![]() 的坐标满足方程
的坐标满足方程![]() ,
,
∴所有顶点![]() 均落在抛物线
均落在抛物线![]() 上
上
(3)[解法一] 由题意可知,顶点![]() 的横、纵坐标分别是
的横、纵坐标分别是
![]()
消去![]() ,可得
,可得 ![]() .
.
为使得所有顶点![]() 均落在抛物线
均落在抛物线![]() 上,则有
上,则有
 解之,得
解之,得 ![]() .
.
∴![]() 所应满足的关系式是:
所应满足的关系式是:![]() .
.
[解法二] 点![]() 的坐标为
的坐标为
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() .
.
又点![]() 的坐标为
的坐标为 且点
且点![]() 也在抛物线上,
也在抛物线上,
![]() ,把点
,把点![]() 代入抛物线方程,解得
代入抛物线方程,解得 ![]() .
.
因此,![]() ,∴抛物线方程为
,∴抛物线方程为![]() .
.
又
∴有顶点![]() 落在抛物线
落在抛物线![]() 上.
上.
∴![]() 所应满足的关系式是:
所应满足的关系式是:![]()

练习册系列答案
相关题目
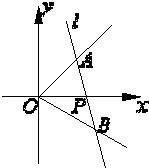 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: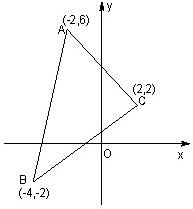 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与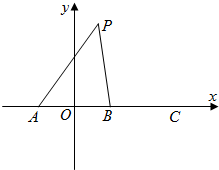 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m. 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为