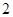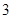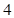题目内容
在直角坐标系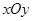 中,点
中,点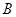 与点
与点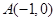 关于原点
关于原点 对称.点
对称.点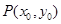 在抛物线
在抛物线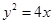 上,且直线
上,且直线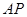 与
与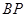 的斜率之积等于-
的斜率之积等于-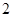 ,则
,则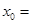 _____________
_____________
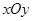 中,点
中,点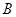 与点
与点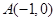 关于原点
关于原点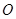 对称.点
对称.点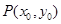 在抛物线
在抛物线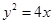 上,且直线
上,且直线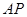 与
与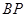 的斜率之积等于-
的斜率之积等于-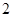 ,则
,则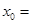 _____________
_____________ -1
-1试题分析:∵点B与点A(-1,0)关于原点O对称,∴B(1,0).
∴kAP=
 ,kBP=
,kBP= ,
,∵kAP•kBP=-2,∴
 ,
,又∵点P(x0,y0)在抛物线y2=4x上,∴
 =4x0
=4x0代入上式得到
 ,化为
,化为 ,解得x0=
,解得x0= .
.∴x0=
 -1.答案为
-1.答案为 -1.
-1.点评:中档题,熟练掌握中心对称性、斜率的计算公式、点在曲线上即满足曲线的方程解出即可。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ( )
( )
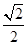
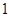
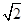
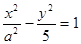 的右焦点为(3,0),则该双曲线的离心率等于 ( )
的右焦点为(3,0),则该双曲线的离心率等于 ( )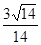

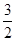 .
.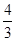
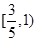


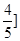
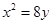 的焦点坐标是 ( )
的焦点坐标是 ( ) 的焦点为顶点,顶点为焦点的椭圆的标准方程是
的焦点为顶点,顶点为焦点的椭圆的标准方程是 



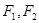 分别是椭圆
分别是椭圆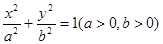 的左右焦点,过
的左右焦点,过 与
与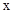 轴垂直的直线交椭圆于
轴垂直的直线交椭圆于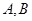 两点,若
两点,若 是锐角三角形,则椭圆离心率的范围是( )
是锐角三角形,则椭圆离心率的范围是( )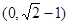


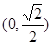
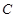 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,其左、右焦点分别为
轴上,其左、右焦点分别为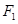 、
、 ,短轴长为
,短轴长为 ,点
,点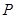 在椭圆
在椭圆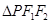 的周长为6.
的周长为6. 的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使
的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使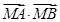 恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.
恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.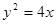 和点
和点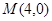 ,
,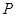 为抛物线上的点,则满足
为抛物线上的点,则满足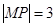 的点
的点