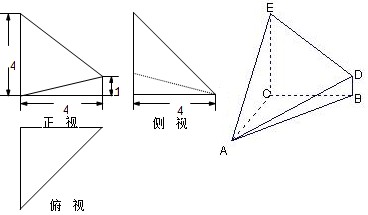
题目内容
在四面体ABCD中，AB＝AD＝BD＝2，BC＝DC＝4，二面角A－BD－C的大小为60°，求AC的长．
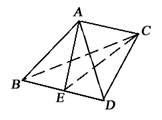
作出二面角A－BD－C的平面角
在棱BD上选取恰当的点
AB＝AD，BC＝DC
解：取BD中点E，连结AE，EC
∵AB＝AD，BC＝DC
∴AE⊥BD，EC⊥BD
∴∠AEC为二面角A－BD－C的平面角
∴∠AEC＝60°
∵AD＝2，DC＝4
∴AE＝
，EC＝
∴据余弦定理得：AC＝
．
在棱BD上选取恰当的点
AB＝AD，BC＝DC
解：取BD中点E，连结AE，EC
∵AB＝AD，BC＝DC
∴AE⊥BD，EC⊥BD
∴∠AEC为二面角A－BD－C的平面角
∴∠AEC＝60°
∵AD＝2，DC＝4
∴AE＝
，EC＝∴据余弦定理得：AC＝
．
练习册系列答案
相关题目
中，
,
，
为
的中点，沿
将△
折起到△
的位置，使得直线
与平面
角。
到直线
的距离为
，求二面角
的大小；
，求
中，二面角
的度数是____________。
,则AD与平面BCD所成的角为( )
与平面
所成角为
，
，则
与
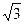，用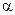
表示∠ASD，求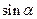
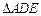沿DE折起，使二面角
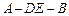的大小为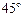
，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小为 .
