题目内容
已知F1, F2是双曲线的两个焦点, Q是双曲线上任意一点, 从某一焦点引∠F1QF2平分线的垂线, 垂足为P, 则点P的轨迹是 （ ）
A．直线 B．圆 C．椭圆 D．双曲线
【答案】
B
【解析】主要考查双曲线的几何性质、圆的定义及标准方程。
解：设O为
，
的中点，延长P交Q于A，连接OP。
据题意知△AQ为等腰三角形，所以Q=QA
∵|Q-Q|=2a，∴|QA-Q|=2a
即A=2a；
又∵OP为△A的中位线
∴OP=a，故点P的轨迹为以O为圆心，以a为半径的圆。选B。
思路拓展：充分利用双曲线定义，借助图形的几何性质，达到了化难为易的目的。
练习册系列答案
相关题目
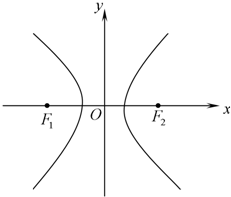
已知F1，F2分别为双曲
-
=1(a＞0，b＞0)的左、右焦点，P为双曲线左支上任一点，若
的最小值为8a，则双曲线的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、（1，+∞） |
| B、（0，3] |
| C、（1，3] |
| D、（0，2] |
的左、右焦点，P为双曲线左支上任一点，若
的最小值为8a，则双曲线的离心率e的取值范围是（ ）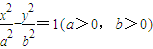
的左、右焦点，P为双曲线左支上任一点，若
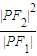的最小值为8a，则双曲线的离心率e的取值范围是（ ）
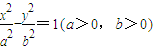的左、右焦点，P为双曲线左支上任一点，若
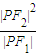的最小值为8a，则双曲线的离心率e的取值范围是（ ）