题目内容
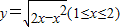 反函数是( )
反函数是( )A.
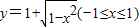
B.
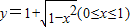
C.
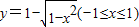
D.

【答案】分析:从条件中函数式 中反解出x,再将x,y互换即得到反函数.
中反解出x,再将x,y互换即得到反函数.
解答:解:在定义域为1≤x≤2,原函数 的值域为-1≤y≤1,
的值域为-1≤y≤1,
∵ ,
,
∴y2=2x-x2,
解得x=1± ,
,
∵1≤x≤2,
∴x=1+ ,
,
∴y=1+ (-1≤x≤1),
(-1≤x≤1),
故选B.
点评:本题主要考查反函数的知识点,首先由已知解析式y=f(x)反求出x=Ф(y),然后交换x、y的位置,最后求出原函数的值域,也就是反函数的定义域.
 中反解出x,再将x,y互换即得到反函数.
中反解出x,再将x,y互换即得到反函数.解答:解:在定义域为1≤x≤2,原函数
 的值域为-1≤y≤1,
的值域为-1≤y≤1,∵
 ,
,∴y2=2x-x2,
解得x=1±
 ,
,∵1≤x≤2,
∴x=1+
 ,
,∴y=1+
 (-1≤x≤1),
(-1≤x≤1),故选B.
点评:本题主要考查反函数的知识点,首先由已知解析式y=f(x)反求出x=Ф(y),然后交换x、y的位置,最后求出原函数的值域,也就是反函数的定义域.

练习册系列答案
相关题目








 反函数是( )
反函数是( )



 的反函数是(
)
的反函数是(
) B.
B.
 D.
D.
 (x≤0)的反函数是
( )
(x≤0)的反函数是
( )
 B.
B.

 D.
D.