Question

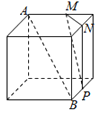
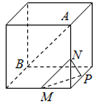
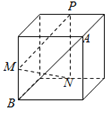
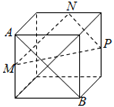
【题目】已知三棱锥的底面是等边三角形，点在平面上的射影在内（不包括边界），.记，与底面所成角为，；二面角，的平面角为，，则，，，之间的大小关系等确定的是（）

A. B.

C. 是最小角，是最大角D. 只能确定，

Answer 1

【答案】C

【解析】

过作PO⊥平面ABC，垂足为，过作OD⊥AB，交AB于D，过作OE⊥BC，交BC于E，过作OF⊥AC，交AC于F，推导出OA＜OB＜OC，AB＝BC＝AC，OD＜OF＜OE，且OE＜OB，OF＜OA，由此得到结论．

解：如图，过作PO⊥平面ABC，垂足为，

过作OD⊥AB，交AB于D，

过作OE⊥BC，交BC于E，

过作OF⊥AC，交AC于F，

连结OA，OB，OC，PD，PE，PF，

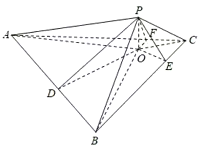
∵△ABC为正三角形，PA＜PB＜PC，

二面角PBCA，二面角PACB的大小分别为，，

PA，PB与底面所成角为，，

∴＝∠PAO，＝∠PBO，γ＝∠PEO，＝∠PFO，

OA＜OB＜OC，AB＝BC＝AC，

在直角三角形OAF中，，

在直角三角形OBE中，，

OA＜OB，∠OAF＜∠OBE，

则OF＜OE，同理可得OD＜OF，

∴OD＜OF＜OE，且OE＜OB，OF＜OA，

∴＜，＜，＞，＜，

可得是最小角，是最大角，

故选：C．