题目内容
设P为双曲线 上的一点,F1,F2是该双曲线的两个焦点,若|PF1|:|PF2|=3:2,则△PF1F2的面积为( )
上的一点,F1,F2是该双曲线的两个焦点,若|PF1|:|PF2|=3:2,则△PF1F2的面积为( )A.

B.12
C.

D.24
【答案】分析:根据双曲线定义得|PF1|-|PF2|=2a=2,所以 ,再由△PF1F2为直角三角形,可以推导出其面积.
,再由△PF1F2为直角三角形,可以推导出其面积.
解答:解:因为|PF1|:|PF2|=3:2,设|PF1|=3x,|PF2|=2x,
根据双曲线定义得|PF1|-|PF2|=3x-2x=x=2a=2,
所以 ,
, ,
,
△PF1F2为直角三角形,其面积为 ,
,
故选B.
点评:本题考查双曲线性质的灵活运用,解题时要注意审题.
 ,再由△PF1F2为直角三角形,可以推导出其面积.
,再由△PF1F2为直角三角形,可以推导出其面积.解答:解:因为|PF1|:|PF2|=3:2,设|PF1|=3x,|PF2|=2x,
根据双曲线定义得|PF1|-|PF2|=3x-2x=x=2a=2,
所以
 ,
, ,
,△PF1F2为直角三角形,其面积为
 ,
,故选B.
点评:本题考查双曲线性质的灵活运用,解题时要注意审题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 上的一点,F1、F2是该双曲线的两个焦点,若
上的一点,F1、F2是该双曲线的两个焦点,若 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( ) B.12 C.12
B.12 C.12 D.24
D.24 上的一点,F1、F2是该双曲线的两个焦点,若
上的一点,F1、F2是该双曲线的两个焦点,若 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( ) B.12 C.12
B.12 C.12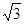 D.24
D.24 上的一点且位于第一象限。若
上的一点且位于第一象限。若 、
、 为此双曲线的两个焦点,且
为此双曲线的两个焦点,且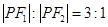 ,则
,则 的周长为 ( )
的周长为 ( ) 上的一点,
上的一点, 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若 ,则
,则 的面积为___________.
的面积为___________.