题目内容
(满分12分)如图,在直线 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为 ,车速为
,车速为 (水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
(水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.

【答案】
当d=2a时,该学生从家出发到达学校所用的最短时间是 .
.
【解析】设该学生从家出发,先乘船渡河到达公路上某一点P(x,0) (0≤x≤d),再乘公交车去学校,所用的时间为t,则 ,求导,利用导数等于零,可得到极值最值.应用题一般考查的函数都是单峰函数.
,求导,利用导数等于零,可得到极值最值.应用题一般考查的函数都是单峰函数.
设该学生从家出发,先乘船渡河到达公路上某一点P(x,0) (0≤x≤d),再乘公交车去学校,所用的时间为t,则 .…5分
.…5分
令 ………8分
………8分
且当 ………9分
………9分
当 ……10
……10
当 时,所用的时间最短,最短时间为:
时,所用的时间最短,最短时间为:
 .……11分
.……11分
答:当d=2a时,该学生从家出发到达学校所用的最短时间是 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线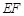 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.
 中,
中, ,
, ,
, ,平面
,平面 平面
平面 ,
, 是线段
是线段 上一点,
上一点, ,
, ,
, .
. 平面
平面 ;
; 与四棱锥
与四棱锥 与
与 ,求
,求 的值.
的值.

 的中点,P为BB1的中点.
的中点,P为BB1的中点. ;
; 所成角的大小;
所成角的大小;